1. 확산 Diffusion
1.1 Up & Down hill diffusion - 확산의 구동력

오늘 포스팅부터는 Phase Transformation 포스팅을 이어가보도록 하겠다.
세세한 설명은 생략하고, 개념과 식 위주로만 정리해놓으려 한다.
기본적인 열역학에 대한 이해를 전제하고 글을 쓰려 하니, 중간중간 궁금한 부분이 있다면
내 티스토리에서 꼭 열역학 포스팅을 참고하길 부탁한다. (아직 내용이 빈약하긴 하지만, 계속해서 업로드하도록 하겠다)
Phase Transformation의 첫 번째 포스팅으로,
확산(Diffusion)을 다뤄보도록 하겠다.
그럼 시작해보자!
1. 확산(Diffusion)
확산(Diffusion)이란 어떤 물리적 요인에 의해서, 혼합물 내의 성분들이 이동하는 현상을 일컫는다.
특히, 우리는 중,고등학교 화학 시간에 농도 차이에 의해 확산이 진행된다고 배웠었는데,
사실은 여러 물리적 요인 중 확산을 일으키는 요인 중 하나가 농도기울기차(concentration gradient)인 것이다.
엄밀하게는 열역학에서, 확산(Diffusion)이란
혼합물의 bulk flow와는 상관 없이 각 물질의 화학퍼텐셜(chemical potential μ)기울기차를
감소시키는 방향으로 발생하는 현상을 일컫는다.
즉, Diffusion의 driving force는 chemical potential gradient라는 것이다.
정확하게는 농도차가 driving force가 아니라는 것이다.
그렇기에, 확산이 농도가 높은 곳에서 낮은 곳으로 진행된다는 일반적인 상식과는 달리
chemical potential이 감소된다면, 농도가 낮은 곳에서 높은 곳으로도 확산이 진행될 수 있다.
1.1 확산의 Driving Force (Thermodynamic Force)
즉, 위에서 설명한 바와 같이,
열역학적으로 확산의 driving force는 chemical potential의 기울기를 이용해 아래와 같이 정의할 수 있다.
F=−(∂μ∂x)T,p
2. Down-hill Diffusion
자 그럼, 일반적인 경우인 Down-hill diffusion,
높은 농도에서 낮은 농도로 확산하는 경우를 살펴보도록 하자.

위 그림에서 보는 바와 같이
①은 A가 많은 곳 (A-rich), ②는 B가 많은 곳(B-rich)이다.
Down-hill Diffusion이란 농도가 높은 곳에서 낮은 곳으로 이동하는 것이므로,
A : ① -> ② 로 이동, B: ② -> ① 로 이동하겠다.
이 상황을 자유에너지-조성(G-X diagram) 그래프로 그려보자.

위 그림은 ①과 ②, 확산이 진행된 후 평형이 이뤄졌을 때를 G-X 그래프에 표시한 것이다.
빨간색은 확산이 진행되기 전 계의 자유에너지 Gsys−initial
파란색은 평형 후 계의 자유에너지 Gsys−eq 을 뜻한다.
2.1 계(System) 전체 자유에너지 G의 변화
그림에서도 보듯, 빨간색 선은 ①, ②의 처음 G를 연결한 것이므로,
우리는 다음과 같은 사실을 알고 있다.
Gsys−initial>Gsys−eq
즉, 전체 계에서 자유에너지는 감소했음을 본다.
2.2 A, B의 chemical potential 변화
이번엔 각 A, B의 chemical potential 변화를 살펴보자.
그림에서는 표기하지 않았으나, ①, ②점에서 그린 접선이 y축과 만나는 교점은
chemical potential을 의미함을 우리는 이미 알고 있다.
(이 내용이 궁금하다면 partial property를 다룬 예전 포스팅을 참고하자.)
즉, 우리는 다음을 관찰 할 수 있다.
μ1A>μ2A
μ1B<μ2B
A의 경우 ①의 μ 가 ②에서 보다 더 크므로, 확산은 ① -> ②로,
B의 경우 ①의 μ 가 ②에서 보다 작으므로, 확산은 ② -> ① 로, 진행됨을 알 수 있다.
바로, chemical potential 차이가 확산의 driving force가 된다는 뜻이다!!
3. Up-hill Diffusion
이번엔, Up-hill diffusion을 살펴보도록 하자.
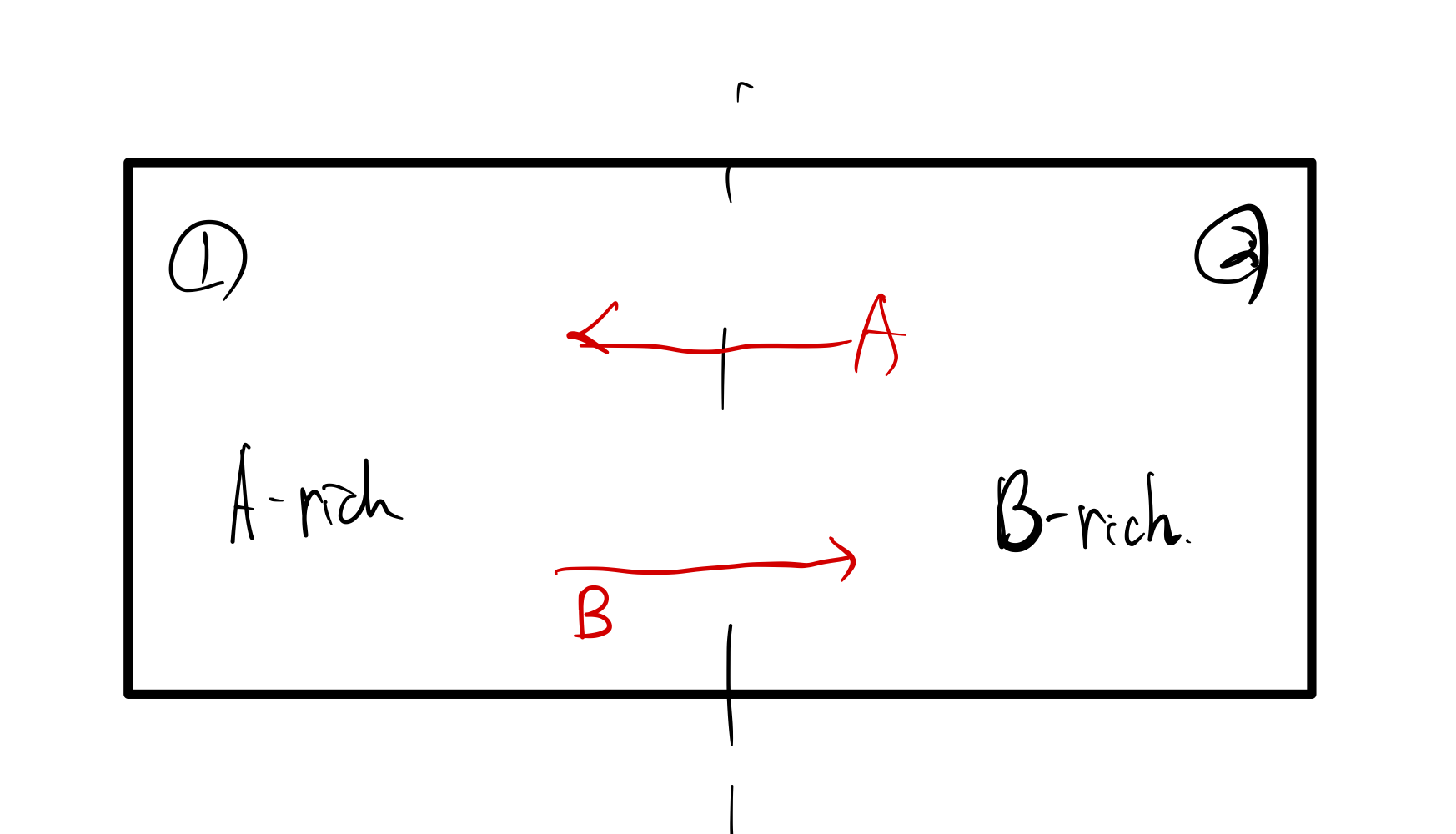
이번에는 반대로,
Down-hill Diffusion이란 농도가 높은 곳에서 낮은 곳으로 이동하는 것이므로,
A : ② -> ① 로 이동, B: ① -> ②로 이동하겠다.
이 상황을 자유에너지-조성(G-X diagram) 그래프로 그려보자.
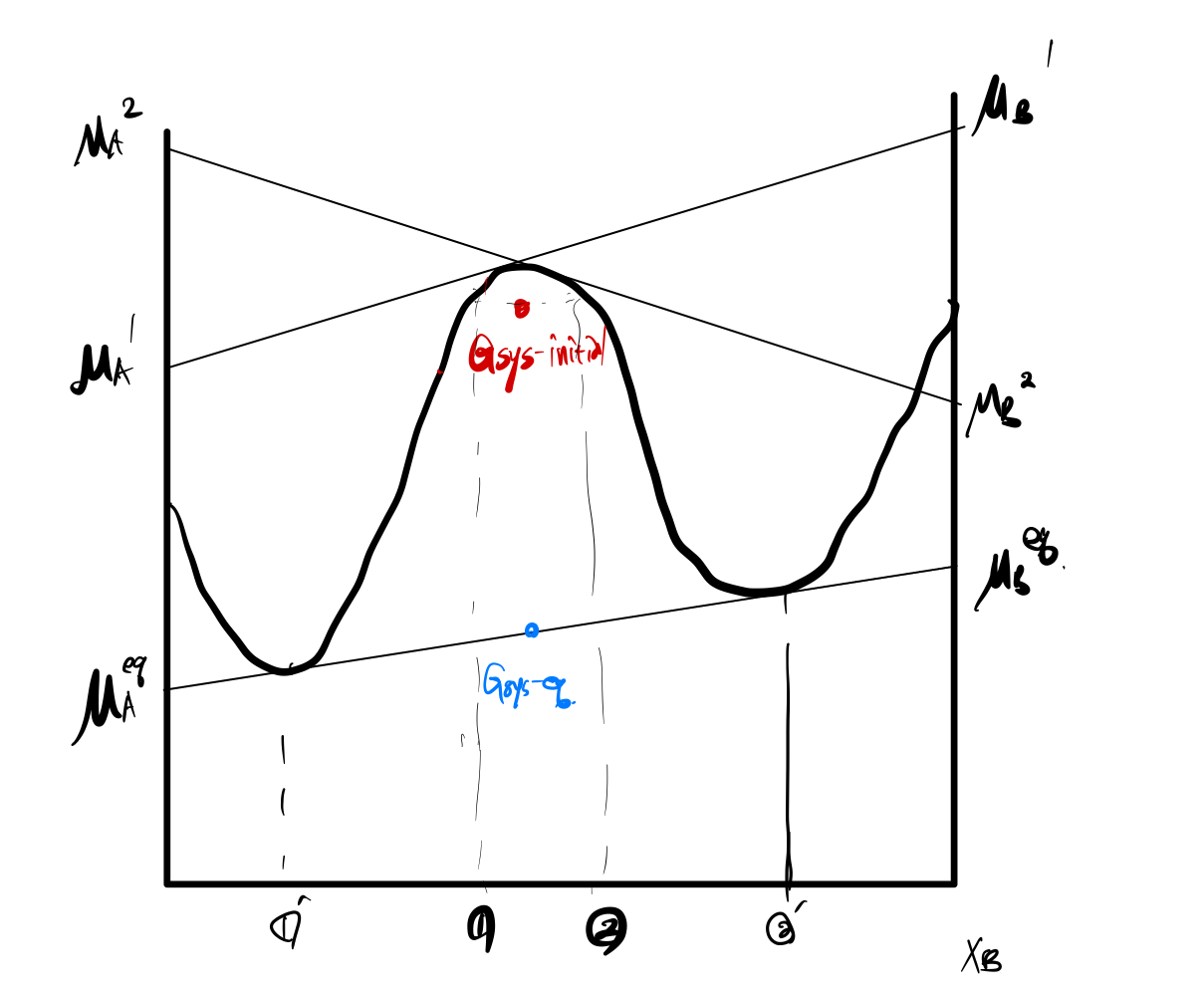
3.1 계(System) 전체 자유에너지 G의 변화
위 2.1 과는 그래프의 개형이 다르다. 과연, 이것이 어떤 차이를 만들지 생각하면서, 아래 설명을 읽어보자.
2.1과 마찬가지로 그림에서도 보듯, 빨간색 선은 ①, ②의 처음 G를 연결한 것이므로,
우리는 다음과 같은 사실을 알고 있다.
Gsys−initial>Gsys−eq
즉, 2.1과 마찬가지로 전체 계에서 자유에너지는 감소했다.
3.2 A, B의 chemical potential 변화
이번엔 각 A, B의 chemical potential 변화를 살펴보자.
위에서 설명했듯, ①, ②점에서 그린 접선이 y축과 만나는 교점은
chemical potential을 의미하므로, (이번엔 그림에 잘 표현되어 있다. 역시 이 내용이 궁금하다면 예전 포스팅을 참고하자.)
다음을 관찰 할 수 있다.
μ1A<μ2A
μ1B>μ2B
A의 경우 ①의 μ 가 ②에서 보다 작으므로, 확산은 ② -> ① 로,
B의 경우 ①의 μ 가 ②에서 보다 더 크므로, 확산은 ① -> ②로, 진행됨을 알 수 있다.
이 역시chemical potential 차이가 확산의 driving force가 됨을 살펴볼 수 있다.
3.3 H of mixing, ΔHmix 가 양수
2의 Down-hill Diffusion에서의 G-X 그래프는 아래로 볼록했었는데,
3의 Up-hill Diffusion의 그래프는 변곡점이 존재하도록, 위로 볼록하게 그렸고,
①, ②도 위로 볼록한 지역에 잡았음을 알 수 있다.
당연하게도 그래프적으로 보면,
위로 볼록한 그래프와 아래로 볼록한 그래프의 접선을 그리게 되면, chemical potential의 대소관계가 바뀔 수 밖에 없다.
자 그러면 이것이 무엇을 의미하는가?
H of mixing, ΔHmix 의 양수인지, 음수인지와 관계가 있다!!
자세한 내용은 열역학 포스팅을 참고하자.
[열역학] 1.3 Regular solution에서의 엔탈피(H), 엔트로피(S), 자유에너지(G) 변화 & Regular solution parameter
열역학 1.3 - Regular solution엔탈피, 엔트로피, 깁스자유에너지 변화 (H, S, G of mixing), Regular solution parameter 지난 포스팅에서는 Ideal solution에서 열역학적 변화특히, 엔트로피와 깁스 자유에너지의 변
gyuuuul.tistory.com
아직 포스팅하지는 않았지만, ΔHmix>0이 되면,
miscibility gap을 가지는 그래프가 만들어 질 수 있다.
아직 설명이 빈약하기는 하나,
추후 설명을 추가하는 것으로 하고,
오늘 포스팅은 여기서 마치도록 하겠다.
그럼 안녕~!!

'전공 공부정리 > Phase Transformation (상변태)' 카테고리의 다른 글
| [PT] 2.1.3 Homogeneous Nucleation / rate (속도) (2) | 2024.11.23 |
|---|---|
| [PT] 2.1.2 Homogeneous nucleation - 2 (0) | 2024.11.23 |
| [PT] 2.1.1 Homogeneous Nucleation - 1 (0) | 2024.11.23 |
| [PT] 1.3.2 Interstitial diffusion / Thermal activation (0) | 2024.11.23 |
| [PT] 1.3.1 침입형 확산 (Interstitial Diffusion) / 픽의 제 1법칙 (Fick's first law) (0) | 2024.11.23 |


