열역학 1.3 - Regular solution
엔탈피, 엔트로피, 깁스자유에너지 변화 (H, S, G of mixing), Regular solution parameter
지난 포스팅에서는 Ideal solution에서 열역학적 변화
특히, 엔트로피와 깁스 자유에너지의 변화(S, G of mixing)를 살펴보았다.
하지만, Ideal solution이라는 가정이 있기 때문에,
조금은 더 현실적으로 존재할 수 있는 solution을 탐구해볼 필요가 있다.
그래서 오늘 포스팅에서는, Ideal solution이 아닌, 그렇다고 완전히 Real한 solution도 아닌
Regular solution을 알아보고, 이 용액 내에서 열역학적 변화(S와 G)를 탐구해보겠다.
지난포스팅이 궁금하면 아래를 참고하자.
2024.09.23 - [전공 공부정리] - [열역학] 혼합 엔트로피와 깁스 자유에너지 변화 - Ideal soultion에서 S & G of mixing구하기
[열역학] 혼합 엔트로피와 깁스 자유에너지 변화 - Ideal soultion에서 S & G of mixing구하기
열역학 - Ideal soultion에서 혼합 엔트로피와 깁스 자유에너지 변화 entropy and Gibbs free energy of mixing 지난 번 포스팅에 이어서 오늘 포스팅에서는Ideal solution에서 혼합 엔트로피와 깁스자유에너지 변
gyuuuul.tistory.com
그럼 시작해보자!!
1. Regular Solution
지난 포스팅에서, Ideal solution은 엔탈피의 변화가 없는
즉, $ \Delta H_{mix} = 0 $ 인 성질을 갖는다고 언급했고, 이를 가정하고 여러 열역학적 변화를 알아보았다.
그럼 만약, 엔탈피의 변화가 생기는 solution이라면 어떻게 될지가 궁금할 터인데,
여러 non-Ideal solution 중,
$ \Delta H_{mix} $ 가 오로지 인접한 두 원자의 bonding energy로만 결정되고,
$ \Delta S_{mix} $ 는 Ideal solution과 같은 값을 갖는 성질의 용액을
Regular Solution이라 부른다.
즉, Regular solution에서 $ \Delta H_{mix} $ 는 bonding energy 등의 계산을 통해
깔끔한 식으로 유도할 수 있다. 유도 과정에서 위에서 언급한 가정이 사용될 것이다.
Regular Soultion 상황을 우리가 공부하는 이유는,
비록 real solution은 아니지만, 간단한 가정을 통해 H of mixing, $ \Delta H_{mix} $ 을 간단히 정리할 수 있기 때문이다.
Ideal Solution에서는 $ \Delta H_{mix} = 0 $ 이었던 것을 생각해보자.
Real Soultion에서의 계산은 복잡하지만, Regular solution에서의 상황을 통해 간략하게 예측할 수 있다.
그럼 함께 알아가보자.
2. Regular Solution의 H of mixing
H of mixing 즉, $ \Delta H_{mix} $ 을 계산해보도록 하자.
위에서 설명했지만, 다시한 번 강조하자면, Regular solution은
$ \Delta H_{mix} $ 가 오로지 인접한 두 원자의 boding energy로만 결정된다.
가정이 필요하다.
A, B 두 원자 사이의 거리와 bond energy는 조성에 무관한, 독립적이라고 생각하자.
아래 그림은 A, B 두 원자들을 mixinig한 상황을 나타낸 것이다.
또한, 다음과 같은 Notation을 사용하자.
| Bond Energy | Number of Bond | |
| A-A | $$ \varepsilon_{AA} $$ | $$ P_{AA} $$ |
| A-B | $$ \varepsilon_{AB} $$ | $$ P_{AB} $$ |
| B-B | $$ \varepsilon_{BB} $$ | $$ P_{BB} $$ |
$ N_A $ : A 원자 개수
$ N_B $ : B 원자 개수
$ Z $ : coordination number(배위수)
2.1 pure A & B 에서 엔탈피 H 구하기
먼저, mixing을 하기 전, pure A 와 pure B 상황에서 엔탈피 H를 생각해보자.
엔탈피 H는 모든 bond energy의 합으로 생각할 수 있으므로,
pure한 A와 B에서는 다음과 같이 정리할 수 있다.
$ H_A = \frac {Z \varepsilon_{AA} } { 2 } N _ { A } $
$ H_B = \frac {Z \varepsilon_{BB} } { 2 } N _ { B } $
조금만 생각해보면 당연하므로, 더이상 설명하지 않겠다.
2.2 mixing 후 엔탈피 H, H of mixing구하기
pure A와 pure B를 위 그림과 같이 mixing을 하였다.
A, B 원자 주변에 있는 각 원자들의 개수에 대해 관계를 가짐을 알 수 있다.
$$ Z \cdot N_{A} = 2 P _ { AA } + P _ { A B } $$
$$ Z \cdot N_{B} = 2 P _ { B B } + P _ { A B } $$
그렇다면 이번엔, mixing 후 엔탈피는 다음과 같이 작성할 수 있다.
$$ H_f = P_{AA} \varepsilon_{AA} + P_{BB} \varepsilon_{BB} + P_{AB} \varepsilon_{AB} $$
위 식에 앞에서 작성한 두 식들을 모두 대입해서 정리해보자.
그럼 다음과 같은 식을 얻을 수 있다.
$$ \begin{align} H_f &= P_{AA} \varepsilon_{AA} + P_{BB} \varepsilon_{BB} + P_{AB} \varepsilon_{AB} \\
&= \frac{Z \varepsilon_{AA}}{2} N_A + \frac{Z \varepsilon_{BB}}{2} N_B + \left( \varepsilon_{AB} - \frac{1}{2} \left( \varepsilon_{AA} + \varepsilon_{BB} \right) \right) P_{AB} \end{align} $$
여기서 $ H_A = \frac {Z \varepsilon_{AA} } { 2 } N _ { A } $, $ H_B = \frac {Z \varepsilon_{BB} } { 2 } N _ { B } $ 임을 생각해보자.
이들은 mixing을 하기 전, pure A 및 pure B의 엔탈피 H이므로, 엔탈피 변화(H of mixing), 즉,
$ \Delta H_{mix} $ 은 다음과 같이 작성할 수 있다.
$$ \Delta H_{\text{mix}} = P_{AB} \varepsilon $$
$$ \varepsilon =\varepsilon_{AB} - \frac{1}{2} \left( \varepsilon_{AA} + \varepsilon_{BB} \right) $$
2.3 Regular solution parameter
1.1.2 에서 얻은 $ \Delta H_{mix} $ 을 새롭게 다시 써보자.
만약에 mixing이 잘 이뤄져서 원자들이 완전하게 random하게 배열되어있다고 생각해보자. (Completely random arrangement)
그러면 A-B bonding의 개수 $ P_{AB} $ 에 대해 다음과 같이 표현할 수 있게 된다.
$$ P_{AB} = Z \cdot N_{A} \frac{N_B}{N_A + N_B} $$
이는, A 원자들 주변의 원자들 중 B가 있을 확률 $ \frac{N_B}{N_A + N_B} $ 을 고려해서 계산한 것이다.
(조금만 생각해보면 당연하므로, 넘어가겠다)
이 식을 1.2.2에서 구한 $ \Delta H_{mix} $ 에 대입해서 정리해보자.
$$ \begin{align} \Delta H_{\text{mix}} &= P_{AB} \left( \varepsilon_{AB} - \frac{1}{2} \left( \varepsilon_{AA} + \varepsilon_{BB} \right) \right) \\ &= \left( \varepsilon_{AB} - \frac{1}{2} \left( \varepsilon_{AA} + \varepsilon_{BB} \right) \right) \cdot Z \cdot N_{A} \frac{N_B}{N_A + N_B} \\ &= \left( \varepsilon_{AB} - \frac{1}{2} \left( \varepsilon_{AA} + \varepsilon_{BB} \right) \right) \cdot Z \cdot N_{AV} X_A X_B \\ &= \Omega X_A X_B \end{align} $$
여기서 마지막 항에서 $ \Omega $ 를 Regular solution parameter 라 부른다.
즉, Regular solution parameter는 다음과 같이 주어지고, 이를 이용해 $ \Delta H_{mix} $ 를 표현하면 다음과 같다.
(위 식에서 $ N_{AV} $ 는 아보가드로 수)
$$ \Omega = \left( \varepsilon_{AB} - \frac{1}{2} \left( \varepsilon_{AA} + \varepsilon_{BB} \right) \right) \cdot Z \cdot N_{AV} $$
$$ \Delta H_{mix} = \Omega X_A X_B $$
3. Regular Solution의 G of mixing
앞서 언급했듯, Regular solution 에서
$ \Delta H_{mix} $ 가 오로지 인접한 두 원자의 bonding energy로만 결정되고,
$ \Delta S_{mix} $ 는 Ideal solution과 같은 값을 갖는다고 하였다.
우리는 방금 1.2에서 $ \Delta H_{mix} $ 을 계산해보았고,
지난 포스팅(궁금하면 여기)에서 Ideal solution의 $ \Delta S_{mix} $와 $ \Delta G_{mix} $을 통계역학적 방법으로 계산했었다.
이 둘을 합치면, 우리는 Regular solution 에서 G of mixing, $ \Delta G_{mix} $을 구할 수 있다.
$$ \Delta H_{mix} = \Omega X_A X_B $$
$$ \Delta S_{mix} = RT \left( X_A \ln X_A + X_B \ln X_B \right)$$
으로부터, 다음과 같다. 이해가 가지 않는다면, 지난포스팅을 참고하자.
$$ \Delta G_{mix} = \Omega X_A X_B + RT \left( X_A \ln X_A + X_B \ln X_B \right) $$
$$ G_f = X_A G_A + X_B G_B + \Omega X_A X_B + RT \left( X_A \ln X_A + X_B \ln X_B \right) $$
4. Regular Solution에서 chemical Potential
이번에는 Regular Solution 에서 화학퍼텐셜(chemical potential)이 어떻게 주어지는지 알아보도록 하자.
chemical potential은 자유에너지의 partial property라는 것은 앞선 포스팅(여기)에서 살펴보았다.
따라서 자유에너지와 chemical potential은 다음과 같은 관계를 가짐을 이미 알고 있다.
$$ G = \mu_A X_A + \mu_B X_B $$
위에서 구한 $ G_f $ 을 아래의 과정을 따라 형태를 바꿔보자.
$$ G_f = X_A G_A + X_B G_B + \Omega X_A X_B + RT \left( X_A \ln X_A + X_B \ln X_B \right) $$
몰분율에 관한 식, $ X_A X_B = X_A X_B \left( X_A + X_B \right) = X_A^2 X_B + X_B^2 X_A $ 을 위에 대입해보자.
$$ G_f = X_A \left( G_A + \Omega (1 - X_A)^2 + RT \ln X_A \right) + X_B \left( G_B + \Omega (1 - X_B)^2 + RT \ln X_B \right) $$
이 식을 위의 chemical potential과 비교해보면, 다음의 chemical potential 식을 구할 수 있다.
$$ \mu_A = G_A + \Omega \left( 1 - X_A \right)^2 + RT \ln X_A $$
$$ \mu_B = G_B + \Omega \left( 1 - X_B \right)^2 + RT \ln X_B $$
이것이 regular solution에서 chemical potential 식이 되겠다. 아래의 ideal solution에서 chemical potential 식과 한 번 비교해보자.
차이점은 Regular solution parameter, $ \Omega $ 항이 추가 되었음을 볼 수 있다.
Ideal solution에서는 $ \Delta H_{mix} = 0 $, 즉 $ \Omega $ = 0 $ 이므로, (위에 대입해보자. 아래와 같아진다.)
위 식이 서로 관련되어 있으며, 타당함을 알 수 있다.
$$ \mu_A = G_A + RT \ln X_A $$
$$ \mu_B = G_B + RT \ln X_B $$
5. 그래프 해석 - $ \Omega $ 부호와 T에 따른 그래프 분류
이제 Regular solution parameter $ \Omega $ 을 이용해서 여러 가지 상황을 판단해보자.
다음 식들로부터 아래 그려진 그래프들을 이해할 수 있을 것이다.
$$ \Delta H_{mix} = \Omega X_A X_B $$
$$ \Delta G_{mix} = \Delta H_{mix} - T \Delta S_{mix} $$
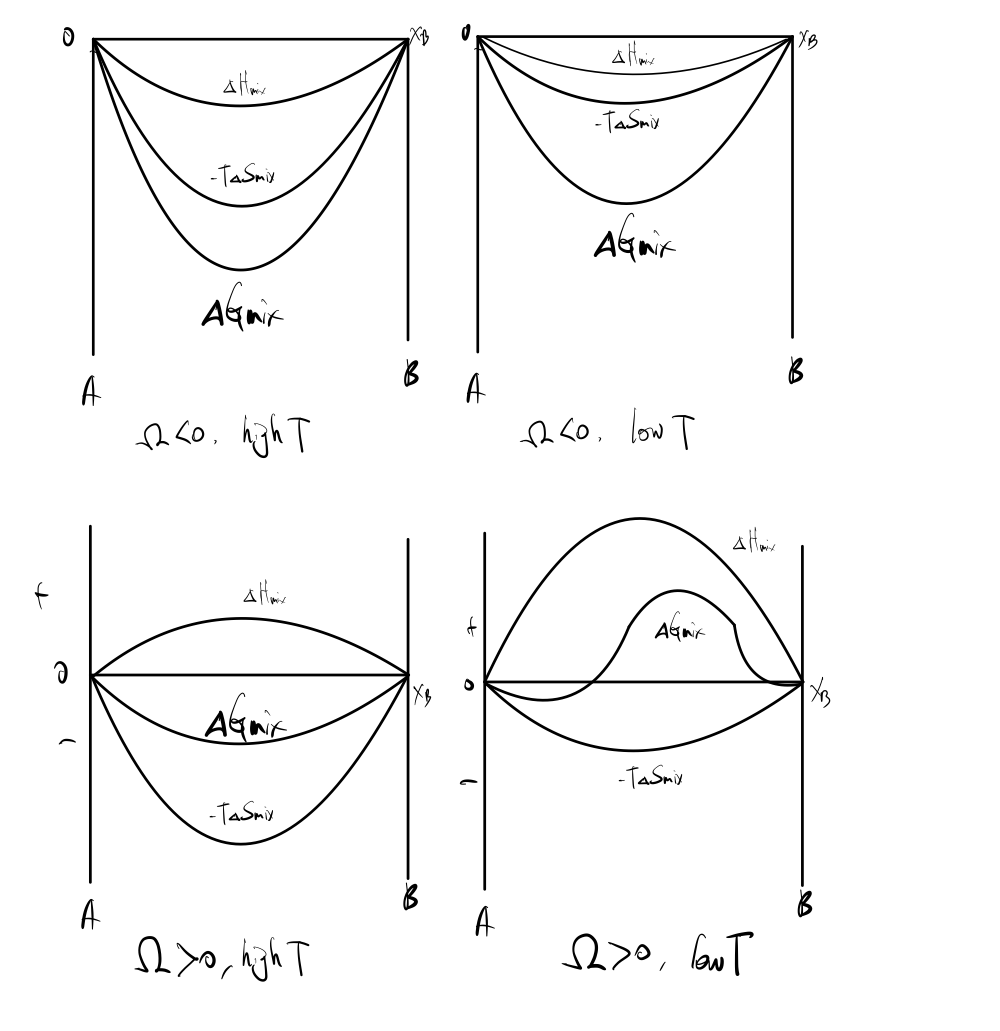
4가지 그래프는 각각, T와 $ \Omega $ 의 부호에 따라 분류해둔 것이다.
식만 보아도, 바로 이해할 수는 있겠으나,
이것의 의미에 대한 이야기는 다음 포스팅(real solution)을 참고하길 바란다.
오늘 포스팅에서는 Regular solution과 열역학적 변화들에 대해 알아보았다.
Regular solution은 ideal 하지는 않지만, 그렇다고 완전히 real한 것은 아니라고 했는데,
다음 포스팅에서는 real solution에서의 변화들을 알아보도록 하겠다.
궁금한 내용이나 질문이 있다면 댓글로 달아주면 친절히 답변해보도록 하겠다.
그럼 다음 포스팅에서 만나요~!!
