1.5 Heterogenous System
Equilibrium, lever rule, G-X curve, phase mixture
오늘 포스팅에서부터는 binary system(성분이 2개)에서 phase diagram(상평형도)가 어떻게 주어지는지,
그 속에 어떤 의미가 숨어있는지 다양한 개념들을 알아보도록 하겠다.
사실은 phase diagram(상평형도)을 처음 포스팅하는 것이기 때문에,
상평형도란 무엇인지, 단일 성분계에서는 어떻게 주어지는지, 삼중점 등을 다뤄야 하지만,
열역학 포스팅을 여태껏, mixture를 다뤄왔기 때문에, 기본 개념설명은 생략하도록 하겠다.
(혹시나 궁금하다면, 다른 블로그를 참고 바란다. 그리고 사실 상평형도는 고등학교 화학시간에 배우기는 한다.)
하여튼, 오늘 포스팅은
ismorphous 상황에서 binary phase diagram과 자유에너지 G 그래프, lever rule 등을 다뤄보도록 하겠다.
그럼 시작해보자.
1. Heterogeneous system
우리는 앞선 포스팅들에서, ideal & regular solution에서의 여러 상태함수들 및 G-X그래프에 대해 살펴보았다.
(내용이 궁금하다면 여기를 참고)
하지만, 앞선 다뤘던 case들은 A와 B가 같은 결정구조(crystal structure)를 갖는 경우로,
G-X함수가 같은 하나의 그래프로 나오는 경우만 다뤘던 것이다.
만약, A와 B가 다른 결정구조(crystal structure)를 가지게 된다면 어떻게 될까?
아마, 두개의 다른 crystal structure가 공존하는 모양새가 될 것이다. 고로, G-X그래프 안에서 두 개의 결정구조를 의미하는 함수가 표현될 것이다.
우리는 이러한 system을 heterogeneous system이라 부른다. 아래 그림을 참고하자.

왼쪽 그림은 앞서 포스팅했던 Ideal solution에서 G-X그래프를 그린 것이고,
오른쪽 그림은 Heterogeneous system에서 G-X그림을 그린 것이다.
오른쪽 그림에서도 알 수 있듯, A는 fcc, B는 bcc 결정구조를 가진다고 하였을 때, phase가 한 개 나오는 Ideal soltuion과 달리,
phase 가 $ \alpha $, $ \beta $ 로 분리가 되어서, 자유에너지 함수가 각각 하나씩 두 개 생기는 것을 볼 수 있다.
2. phase mixture와 G, lever rule
두 개의 phase가 섞인 mixture에서 자유에너지는 어떻게 주어질까?
$ \alpha $ 상은 몰분율 $ X_B^\alpha $, 자유에너지 $ G^\alpha $ 를 갖고,
$ \beta $ 상은 몰분율 $ X_B^\beta $, 자유에너지 $ G^\beta $ 를 갖는다고 하자.
이 둘이 섞여서, $ \alpha + \beta $ 가 되고, 몰분율 $ X_B^o $ 이 때 mixture 자유에너지를 $ G(\alpha + \beta) $ 가 된다.
이를 아래 그래프를 표현해보자.

mixture의 자유에너지 $ G(\alpha + \beta) $ 는 $ G^\alpha $, $ G^\beta $ 점을 연결한 직선의 내분점과 같다.
따라서 내분을 이용하면, 다음의 관계식을 작성할 수 있다.
$$ G(\alpha + \beta) = \frac{X_B^\beta - X_B^o}{X_B^\beta - X_B^\alpha } G^\alpha + \frac{ X_B^o - X_B^\alpha }{X_B^\beta - X_B^\alpha } G^\beta $$
이는 $ \alpha $ 상과 $ \beta $ 상의 조성비율이 $ X_B^\beta - X_B^o : X_B^o - X_B^\alpha $ 로 주어진다는 것을 의미한다.
우리는 이를 Lever rule 이라 부른다.
이 Lever rule에 대한 더 디테일한 이야기는 추후 포스팅을 통해 설명해보도록 하겠다.
그렇다면, 이를 이용해 Heterogeneous system에서 평형을 어떻게 설명할 수 있을까? 그리고 왜 발생할까?
같이 알아가보자.
3. Equilibrium in Heterogeneous System
아래의 그림처럼 heterogeneous system 의 G-X 그래프가 주어졌다.
초기 상황은 조성이 $ X_0 $ 인 어떤 단일 상(homogeneous phase) 용액,
즉 $ \alpha $ 상 ($ G_0^\alpha $)혹은 $ \beta $ 상 ($ G_0^\beta $)용액이라 하자. $ ( G_0^\beta > G_0^\alpha ) $

만약, 단일 상(homogeneous phase) 이 A와 B 원자가 서로 교환되면서 \( \alpha + \beta \) 로 상이 분리된다면,
위의 2번에서 작성한 식을 만족하면서, 각 상의 자유에너지가 위 그림처럼 $ G_1^\alpha $, $ G_1^\beta $ 로 표현될 것이다.
고로 전체 자유에너지 $ G_1 $ 은 $ G_0^\alpha $, $ G_0^\beta $ 에 비해 작아짐을 확인할 수 있다.
$$ G_1 < G_0^\beta \; \; or \; \; G_0^\alpha $$
이러한 상 분리가 계속진행되어서, 최종적으로 위 그림의 $ G_e^\alpha $, $ G_e^\beta $ 점에 도착한다면,
전체 자유에너지 $ G_e $ 는 최소에너지가 될 것이다. 따라서 더 이상 상 분리가 진행될 이야가 없으므로,
이 때를 Equilibrium 지점이라고 이야기할 수 있다.
수학적으로 생각해보면 당연하지만,
이 Equilibrium 지점은 두 그래프의 공통접선(common tangent line)의 교점이 된다.
화학평형이란 multiphase에 대해서 multicomponent가 $ \mu , \; a $ 에 대해 다음을 만족하는 것을 말한다.
$$ \mu_i^\alpha = \mu_i^\beta = \mu_i^\gamma = \dots $$
$$ a_i^\alpha = a_i^\beta = a_i^\gamma = \dots $$
즉, 이 그래프에 적용하면 다음을 우린 얻을 수 있다.
$$ \mu_A^\alpha = \mu_A^\beta $$
$$ \mu_B^\alpha = \mu_B^\beta $$
$ \mu $ (chemical potential)는 그래프의 접선이 y축과 만날 때, 그 값을 의미했었다.
위 그림에서도 보듯 공통접선의 y축 교점이 각 A와 B의 chemical potential임을 알 수 있다.
(이 내용이 궁금하다면, 여기로. a: activity에 대한 설명은 앞선 포스팅에서 하지 않았으므로 생략하도록 하겠다.)
4. phase 영역 표시
이제까지 Heterogeneous system 에서의 평형 및, 상의 분리에 대해 다루고 G-X 그래프에 그려보았다
그렇다면, phase의 영역은 G-X 그래프에서 어떻게 주어질까? 아래를 살펴하자.
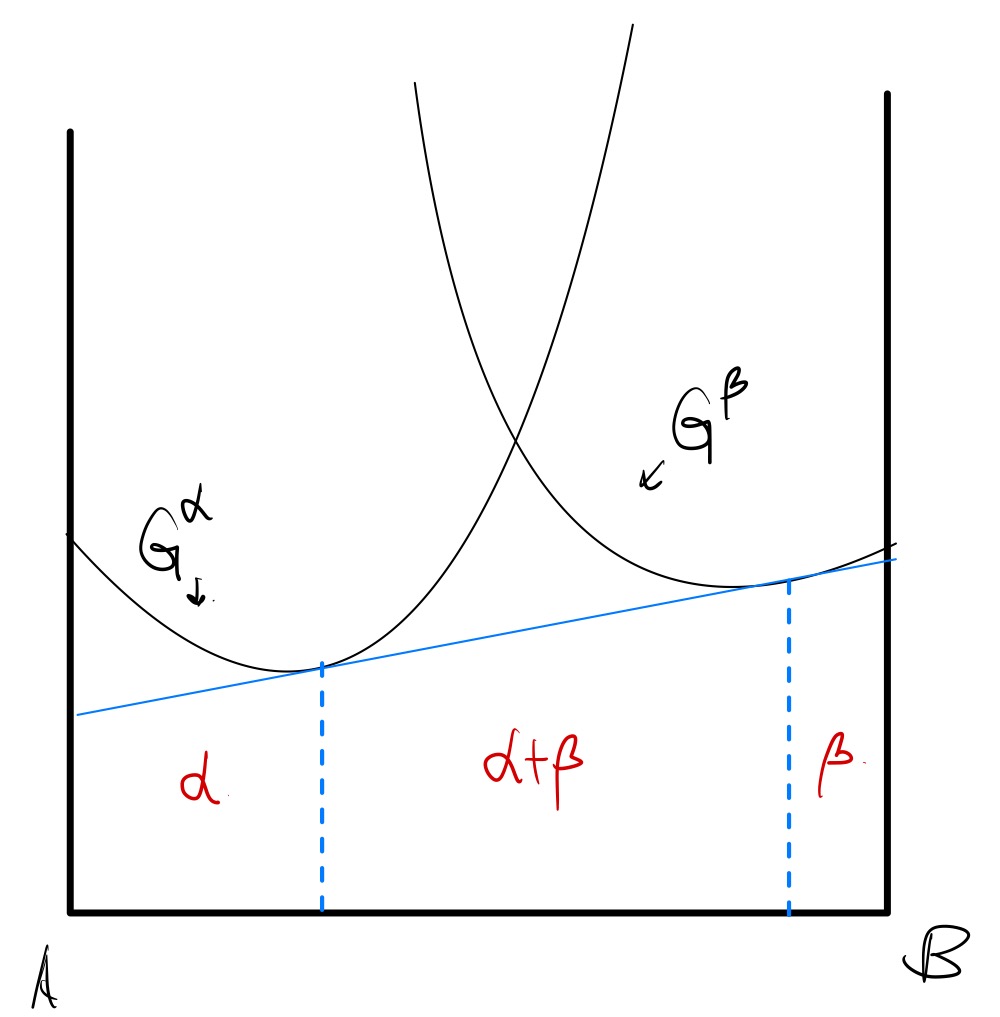
3번에서 살펴보았듯, 공통접선에서 두 접점 안 쪽, $ \alpha + \beta $ 영역은
두 상이 분리되어 평형을 이루고, 공존함을 알 수 있다. 이 상의 비율은 lever rule 로 계산된다는 것도 2번에서 살펴보았다.
두 접점 바깥 영역들은 각각 $ \alpha $ 와 $ \beta $ 가 존재하는 영역이다.
이 G-X 그래프를 잘 이해하는 것이 정말정말!!! 중요하겠다.
오늘 포스팅에서는 Heterogeneous system과 평형, lever rule, G-X 그래프 등등 정말 중요한 개념들을 알아보았다.
앞으로의 phase diagram에 대해 집중적으로 포스팅할 계획인데,
이를 이해하는데 정말 기본이 되는 개념 되시겠다
다음 포스팅부터 binary phase diagrm 을 시작으로 phase diagram에 대해 포스팅하도록 하겠다.
궁금한 내용이나 질문이 있다면 댓글로 달아주면 친절히 답변해보도록 하겠다.
그럼 다음 포스팅에서 만나요~!! 안녕~~!!




