열역학, 그 중 Binary solutions
- 부분성질(Partial Property), 화학 퍼텐셜(chemical potential), 깁스-듀헴 방정식(Gibbs - Duhem equation)

오늘 포스팅부터는
열역학을 공부하면서 중요한 것들을 뽑아 깔끔하게 정리해서 기록해볼까 한다.
아무래도 전공과목이다 보니, 개념에 대한 자세하고 친절한 설명을 하기에는 너무 글이 길어질 것 같아
기본개념은 생략하고 중요한 내용만을 위주로만 포스팅해보려 한다.
일반물리, 화학, 미적분학 수준의 개념을 알고 있다는 전제 하에, 글을 작성해보겠다.
다소 양해를 부탁한다.
그래도 오늘 포스팅에서는
부분 성질, Partail molar property에 다뤄보려한다.
이 부분성질은 열역학에서 여러 물질을 섞을 때, (mixture)
화학포텐셜(chemical potential) 등 정말 중요하게 사용되는 개념이니 꼭 알아두어야 한다.
그럼 한번 시작해보자!!
1. Partial property
어떤 시스템 안에서, 어떤 열역학 함수 Y는
온도(T), 압력(P), 몰 수(조성 - n) 을 이용해 다음과 같이 표현할 수 있다.
$$ Y = Y (T, P, n_1, n_2, \cdots, n_i, \cdots) $$
이러한 함수 Y가 주어졌을 때,
열역학에서 부분 성질, partial property는 다음과 같의 정의한다.
$$ \bar{Y}_A=\left(\frac{\partial Y}{\partial n_i}\right)_{P, T, n_j} $$
수학적으로 보듯, 부분 성질은
온도(T)와 압력(P), 그리고 나머지 성분의 몰 수($ n_j $)가 일정할 때,
성분 i 몰 수의 미소 변화에 의한 어떤 열역학 함수 Y의 미소 변화량이다.
이 Y에는 부피(V), 깁스 자유에너지 (G), 엔탈피(H) 등이 될 수 있다.
기호를 잘 익혀두도록 하자.
위의 overbar가 붙으면, partial property가 된다.
2. 화학퍼텐셜 (Chemical Potential)
위의 Partial property를 이용해, 화학퍼텐셜을 정의한다.
$$ \mu_i = \left(\frac{\partial G}{\partial n}\right)_{p, T, n_j} $$
$$ \mu_i = \bar{G_i} $$
3. Summabilty relation
직관적으로 당연해 보이지만,
이해하기 어려운 개념중에 하나가 Summability relation이다.
Partial property와 열역학적 함수 Y 사이의 관계를 나타낸 것인데, 다음과 같다.
$$ Y=\sum_{i=1}^q x_i \bar{Y}_i $$
여기서 $ x_i $ 는 i의 몰분율(mole fraction)을 의미한다.
이는 즉, Y의 각 성분별 partial property를 모두 알고, 그 조성을 알고 있다면,
선형적인 sum을 통해 전체 Y를 구할 수 있다는 말이다.
부분압력법칙 등을 생각하면 너무나도 당연해 보이지만, 증명이 필요하다.
사실 대다수의 책에서 이 부분을 크게 설명하지 않고, 당연한 사실로 언급하고 넘어가지만
정말 중요한 개념인 만큼, 수학적 증명도 알아두면 좋겠다.
추후에 이 부분은 정리해서 보충설명을 해보도록 하고,
궁금하다면, wikipedia - partial molar property를 참고하면 된다.
4. Gibbs-Duhem Equation
열역학에서 굉장히 중요한 깁스-듀헴 방정식을 유도해보자.
앞서 언급한 어떤 열역학적 함수 Y를 가지고 와서, 전미분 해보자.
$$ \begin{aligned} &Y=Y\left(T, P, n_1, n_2, \cdots, n_i, \cdots\right)\\ &d(Y)=\left[\frac{\partial(Y)}{\partial P}\right]_{T, n} d P+\left[\frac{\partial(Y)}{\partial T}\right]_{P, n} d T+\sum_i\left[\frac{\partial(Y)}{\partial n_i}\right]_{P, T, n_j} d n_i \end{aligned} $$
위에서 언급한 partial property 기호를 사용해 다음과 같이 표현하자.
$$ d(Y)=n\left(\frac{\partial Y}{\partial P}\right)_{T, x} d P+n\left(\frac{\partial Y}{\partial T}\right)_{P, x} d T+\sum_i \bar{Y}_i d n_i $$
이번에는 summability relation을 가지구 와서, 미분하자.
그럼 다음과 같은 식을 얻는다.
$$ d Y =\sum_i x_i d \bar{Y}_i+\sum_i \bar{Y}_i d x_i $$
위 두 식을 연립해서 정리하면, 다음의 식을 얻는다.
$$ ( \frac { \partial Y} { \partial P} ) _ { T , x } d P + ( \frac { \partial Y } { \partial T } ) _ { P, x } d T - \sum _ { i } x _ { i } d \bar{Y} _ { i } = 0 $$
우리는 이를 깁스-듀헴 방정식 Gibbs-Duhem Equation이라 부른다.
식을 보면 알 수 있듯, 특별히 constant 한 온도(T), 압력(P)조건에서는 다음이 성립한다.
$$ \sum _ { i } x _ { i } d \bar{Y} _ { i } = 0 $$
정말 유용한 식이다.
몰분율과 어떤 열역학적 함수 (화학 퍼텐셜, 엔탈피 등)이 서로 간단히 연관되어 있기 때문이다.
특히, 화학퍼텐셜(chemical potential)을 사용하여 정리한 형태를 자주 사용하게 된다.
(다음 포스팅에서도 이를 다룰 것이다.)
5. 부분성질의 그래프적 의미
이제, 부분성질 Partial Property 이 그래프적으로 어떤 의미를 가지는지 알아보자.
다음 포스팅에서 다룰, 상평형 그림에서 정말 중요한 내용이니, 꼭 기억해두자.
쉽게 알아보기 위해서, 2 물질 시스템 - binary system을 생각해보자.
Summability relation에 따라 다음이 성립한다.
$$ Y = X _ { 1 } \bar{Y _ { 1 }} + X _ { 2 } \bar{Y _ { 2 }} $$
이를 미분해보자.
$$ d Y = \bar{Y _ { 1 }} d x _ { 1 } + x _ { 1 } d \bar{Y _ { 1 }} + \bar{Y _ { 2 }} d x _ { 2 } + x _ { 2 } d \bar{Y _ { 2 }} $$
Gibbs-Duhem equation을 적용하면, 두 항을 소거할 수 있다.
$$ d Y = \bar{Y_{ 1 }} d x _ { 1 } + \bar {Y _ { 2 }} d x _ { 2 } $$
binary system이기 때문에 $ x_1 + x_2 = 1 $이 언제나 성립한다.
따라서 $ dx_1 + dx_2 $ 역시 당연히 성립한다.
이 식과 Summability relation을 위 식에 대입해서 적절히 정리하면, 다음을 얻는다.
$$ \bar {Y _ { 1 }} = Y - X _ { 2 } \frac { d Y } { d x _ { 2 } } $$
$$ \bar { Y_ { 2 }} = Y + X _ { 1 } \frac { d Y} { d x _ { 2 } } $$
완성이다!! 이 식을 잘 살펴보자. 수학적으로 중요한 의미를 가진다!!
정답은 바로, 아래 그림에 그려져 있듯
$ X_2 $ 지점에서 Y 함수에 대한 접선(tangent line, 빨간 접선)을 그렸을 때,
Y축 교점들이 바로!! 1과 2 각각의 부분성질 Partial property가 된다.
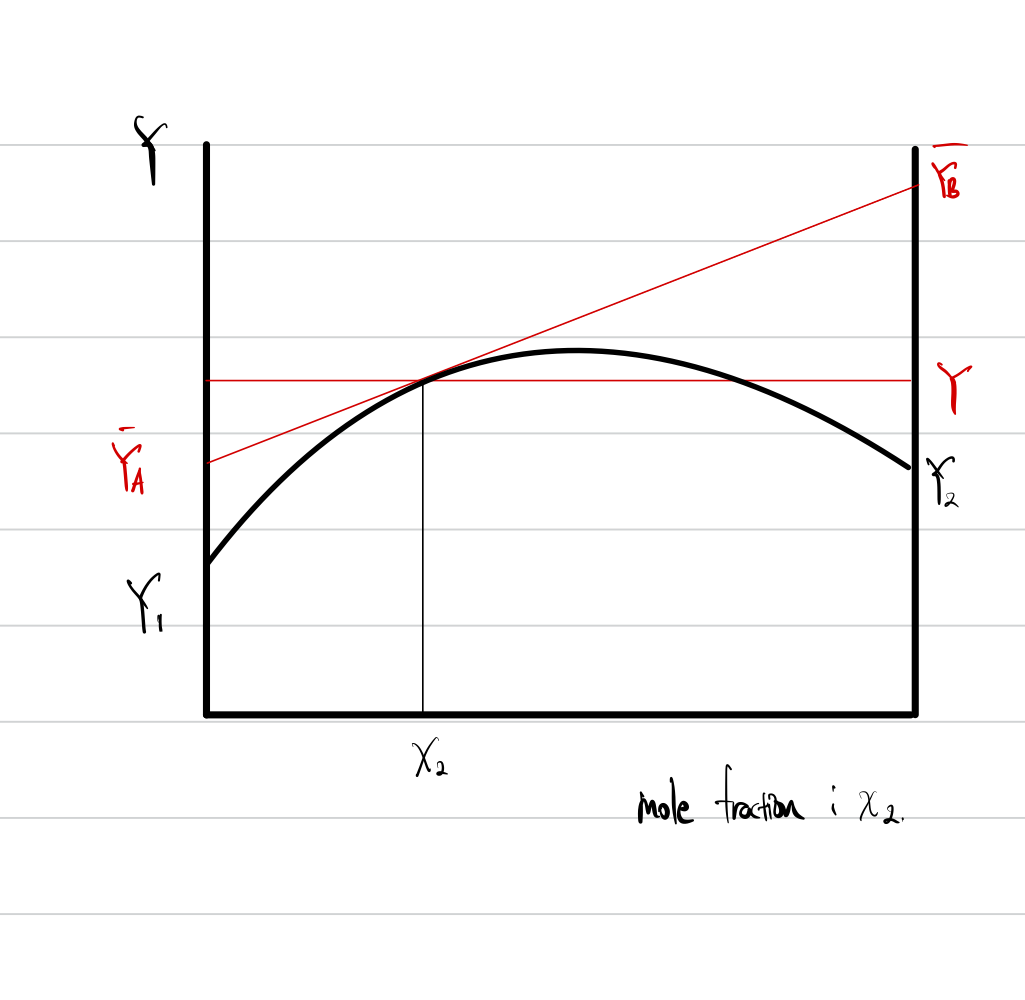
정말 중요한 그래프이다!!
Y가 깁스 자유에너지(G) 일 때, 정의에 따라 Partial Property는 화학퍼텐셜(chemical potential)이 되는데,
상평형 그림을 그릴 때, 정말 자주 보게 될 것이다!!
그러니 꼭, 잊어버리지 말고 기억하도록 하자.
오늘 포스팅에서부터 열역학 포스팅을 시작해보려 하는데,
그 중 첫 번째로 여러 물질이 혼합된 mixture에서 정말 중요한
부분 성질, 깁스-듀헴 방정식 등 기본 개념들을 정리해보았다.
앞으로의 포스팅에서는
그래프 해석, 상평형 그림 등을 다뤄보도록 할 것이니,
많은 기대를 부탁한다.
궁금한 것이나 질문사항이 있다면 언제든 댓글을 남겨주면,
시간이 되는대로 친절히 답변을 해보도록 노력해보겠다.
그럼 안녕~~!!

'전공 공부정리 > 열역학' 카테고리의 다른 글
| [열역학] 1.5 비균일계(Heterogenous System) 에서의 평형, lever rule (2) | 2024.11.18 |
|---|---|
| [열역학] 1.4 Real Solutions에서의 열역학적 변화 및 분류 (0) | 2024.11.17 |
| [열역학] 1.3 Regular solution에서의 엔탈피(H), 엔트로피(S), 자유에너지(G) 변화 & Regular solution parameter (1) | 2024.10.07 |
| [열역학] 1.2 혼합 엔트로피와 깁스 자유에너지 변화 - Ideal soultion에서 S & G of mixing구하기 (0) | 2024.09.23 |



