2.3 Solidification of Single-Phase Alloys
2.3.2 Non-equilibrium Solidification - Scheil equation

지난 포스팅부터, 단일 상 (Single phase) alloy의 Solidification에 다뤄보고 있다. single phase alloy 의 solidification을 다음의 세 경우로 구분할 수 있었다. (지난 포스팅 참고)
[PT] 2.3.1 Solidification of Single-Phase Alloys / Equilibrium Solidification
2.3 Solidification of Single-Phase Alloys2.3.1 Equilibrium Solidification 오늘 포스팅부터는 Alloy의 Solidification에 다뤄보도록 하겠다.2.3 에서는 단일 상 (Single phase) alloy의 solidification 에 대해, 2.4 에서는 Eutectic
gyuuuul.tistory.com
- 1. 고체와 액체가 완벽하게 섞이는 경우(perfect mixing):
즉, 평형을 언제나 이룸(Equilibrium Solidification) - 2. 고체에서는 확산이 일어나지 않고(평형이 아님, no diffusion),
액체는 완벽하게 섞이는 경우(perfect mixing) - 3. 고체에서 확산이 일어나지 않고(평형이 아님, no diffusion),
액체는 확산이 일어나며 섞이는 경우 (diffusional mixing)
그 중 1번은 Equilibrium Solidification, 나머지 2번과 3번은 non-equilibrium solidification이라고 부른다.
1번은 지난 포스팅에서 다뤄보았고, 이번 포스팅에서는 2번의 non-equilibrium solidification 와, 이 경우에서 lever rule 에 해당하는 Scheil equation을 다뤄보도록 하겠다.
그럼 시작해보자!
1. No Diffusion in Solid, Perfect Mixing in Liquid
이 경우에는, cooling을 급격하게 해서, 액체는 충분히 섞였는데(perfect mixing),
고체는 섞이지 못한 경우를 살펴보자. 즉, 고체 내에서 확산이 일어나지 못한다. (no diffusion)
여기서 주의할 점은, 액체가 충분히, 잘 섞였다는 것이다! (well stirring)
만약, 잘 섞이지 못한 액체라, diffusion이 발생하는 경우라면, 다음 포스팅에서 다룰 내용이다.
먼저, 아래의 상평형도를 살펴보자.

저번 포스팅, Equilibrium soldification의 경우와는 다르게,
¯Xs (평균 조성)가 추가되었음을 확인할 수 있다.
이것이 무얼 의미하고, 왜 추가되었는지를 알아가보자.
1.1 미세구조 (Microstructure) 관찰
먼저, 미세구조(microstructure)를 관찰해보자.
위 상평형도에서 X0 조성을 갖는 액체를 빠르게 cooling 했더니,
액체는 충분히 섞였는데(perfect mixing), 고체는 확산이 일어날 수 없었다고 하자.
그러면, 고체는 cooling과정에서 정출되면서,
확산(diffusion)이 일어나지 않아, 평형을 이루지 못하고, 그 조성을 그대로 유지하게 된다.
따라서, 아래 그림과 같이, 각 껍질의 조성이 모두 다른, 고체가 연속적으로 정출되게 된다.

위의 상평형도에서, 온도가 내려갈 때, Solidus line을 추적해보게 되면,
고체가 나중에 정출될 수록 조성이 높아짐을 본다. X↑
따라서 위 그림에서는, 중심에서 바깥쪽으로 갈 수록 나중에 정출된 것이므로 조성이 높아진다.
반면, 액체는 충분히 섞였으므로, 고체와 같은 분화가 없음을 알 수 있다.
바로 이런 경우를 고체가 평형을 이룰 수 없었다고 말한다. (no diffusion, non-equilibrium)
1.2 조성-단면 알아보기
위 상평형도에서, T1−δ,T2,TE 온도에서의 alloy 단면을 알아보자.
( X 축은 distance, y축은 조성 X )

Equilibrium soldification와는 달리, 고체 쪽 선이 일정하지 않음을 한눈에 알아 볼 수 있다.
특히 T2 에서 명확히 드러나듯, 고체 쪽 선이 상승하고 있음을 볼 수 있다.
위에서 살펴보았듯, 고체에서 확산(diffusion)이 일어나지 않아, 평형을 이루지 못하고,
조성을 그대로 유지하기 때문에 solidus line처럼 상승하는 것이다.
따라서, 고체의 평균 조성: ¯XS 은 언제나 XS 보다 작게 된다.
(위의 상평형도, 빨간색 선을 살펴보자)
¯XS<XS
반면에, 액체는 X0/k 을 뛰어 넘어서, Eutectic point XE 까지 도달할 수도 있게 된다.
위의 세 번째 단면도, 온도 TE 에서 그린 것을 살펴보자.
(위 상평형도에서 ¯XS 가 TE 에 도달했을 때에도, X0를 넘지 못하였으므로, Eutectic 온도 TE 까지, solidification이 계속 진행되었음을 의미한다.)
1.3 non-equilibrium lever rule (coring structure): Scheil Equation
이러한 solidification의 문제는 바로, 평형을 이루지 못하기 때문에 Lever rule을 적용할 수 없다는 것이다.
그래서 새로운 형태의 mass balance를 나타내는 식을 도출해야 된다.
어떤 온도 T 에서 cooling이 진행되어도, 다음의 관계는 무조건 만족하게 된다.
액체에서 분출된 용질 양 = 액체의 용질 증가량
무슨 말인지 잘 감이 안온다면, 아래의 조성 그래프를 살펴보자.
fs : 고체의 부피 비율, fL : 액체의 부피 비율 ( fs+fL=1 )
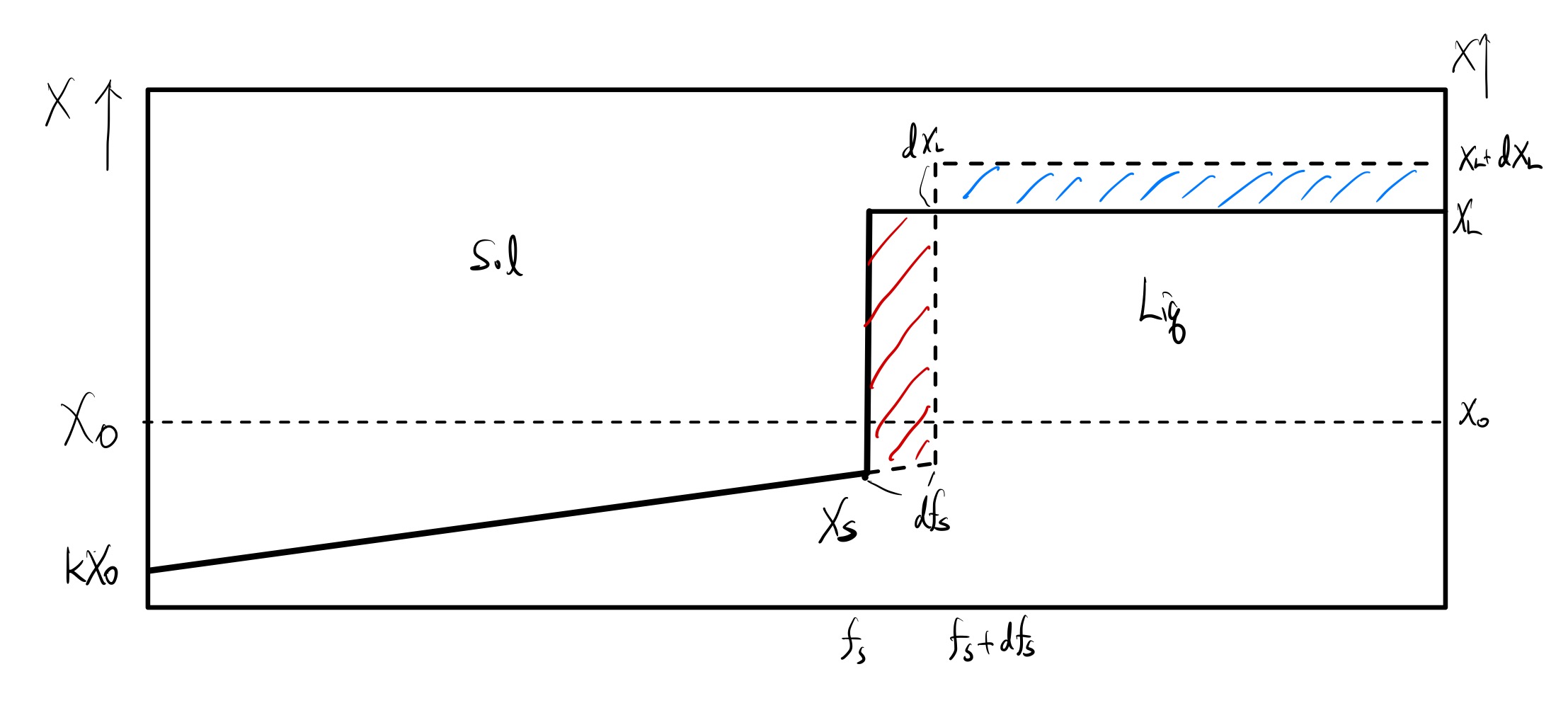
액체에서 분출된 용질 양은 (XL−XS)dfS, 빨간색 영역의 넓이고,
액체의 용질 증가량 (1−fS)dXL, 파란색 영역의 넓이다.
즉, 두 영역의 넓이가 같다는 식을 세우게 되면, 다음을 만족한다.
(XL−XS)dfS=(1−fS)dXL
fS=0 에서 초기조건: XS=kX0 , XL=X0 과
Xs=kXL, fs+fL=1 를 이용해서 위 식을 풀어보자.
∫fS0dfS1−fS=∫XLX0dXLXL−XS=∫XLX0dXLXL−kXL=∫XLX0dXLXL(1−k)
∫fS0(1−k)(−1)dln(1−fS)=∫XLX0dlnXL
lnXLX0=(k−1)ln(1−fS)
∴
X_S = k X_0 (1 - f_S)^{(k - 1)}
이를 non-equilibrium lever rule (Scheil equation)이라 한다.
만약, k < 1 라면, eutectic이 반드시 발생함을 알 수 있다. 위의 Scheil equation을 보면,
f_S \to 1 , f_L \to 0 로부터,
X_L , X_S \to \infty
이므로 반드시, X_L 은 X_E 에, X_S 는 X_{max} 에 도달하기 때문에 그렇다.
1.4 Supercooling과 Microstructure
(추후 그려넣도록 하겠다.)
오늘 포스팅에서는 non-equilibrium solidifcation, 그 중에서도 no diffusion in solid, perfect mixing in liquid 경우를 살펴보았다.
다음 포스팅에서는 남은 한 개의 non-equilibrium solidifcation (위의 3번) 을 다뤄보도록 하겠다.
궁금한 점이 있다면, 언제든 댓글로 질문을 달아주면 성실히 답변해보도록 하겠다.
그럼 안녕~!!




