2.1 Nucleation
2.1.4 Heterogeneous nucleation

지난 포스팅까지 Homogeneous Nucleation에 대해 다뤄보았는데,
오늘 포스팅부터는 Heterogeneous Nucleation에 대해 다뤄보고자 한다.
1. Heterogeneous nucleation
solidification이 어떤 mould 안에서 진행될 때, mould 표면에 붙어서 핵을 형성할 때를 Heterogeneous Nucleation이라 한다.
단, 다음과 같은 가정을 하자.
- $ \gamma_{ML} $ : isotropic
- mould 표면이 상대적으로 flat하다.
- spherical cap (돔 혹은 볼록렌즈 같은 거) 모양을 가진다.
아래 그림을 참고하자.


2. Heterogeneous Nucleation의 자유에너지 변화, $ \Delta G_{\text{het}} $
저번 Homogeneous nucleation 포스팅 내용을 다시 한 번 remind해보자.
\[ \Delta G^* = \left( \frac{16 \pi \gamma_{SL}^3 T_m^2}{3 L_v^2} \right) \frac{1}{(\Delta T)^2} \]
이로부터, 만약 mould 표면에 nucleation이 진행되면서 Liquid와 만나는 면적이 줄어들게되고,
그로인해 \( \gamma_{SL} \downarrow \) 이면,$ \Delta G^* $ 가 낮아지면서, Nucleation이 쉽게 형성될 것이다.
아래 그림은 Mould에 붙은 solid를 그린 것이다. 함께 살펴보자.

여기서
$ \theta $ : 접촉각(contact angle)
$ r $ : solid의 반지름 (cap radius)
$ A_{SL} , \; \gamma_{SL} $ : solid 상부에서 고체(solid)와 액체(liquid)사이 면적과 표면에너지(surface energy)
$ A_{SM}, \; \gamma_{SM} $ : solid 하부에서 고체(solid)와 Mould사이 면적과 표면에너지(surface energy)
$ \gamma_{ML} $ Mould와 액체(liquid)사이 표면에너지(surface energy)
이 때, 표면에너지들 사이의 관계는 접촉각 $ \theta $를 이용해 다음과 같이 표현된다.
이를 영의 방정식 (Young's equation)이라 부르는데, 이 것이 궁금한 사람들은 구글에 Young's equation과 contact angle을 검색해보자. 꽤 자세한 설명이 많이 나온다. (여기서 의미설명이나 유도는 생략하겠다)
\[ \gamma_{ML} = \gamma_{SL} \cos \theta + \gamma_{SM} \]
\[ \cos \theta = (\gamma_{ML} - \gamma_{SM}) / \gamma_{SL} \]
이 때, heterogeneous nucleation에서 자유에너지 변화는 다음과 같이 쓸 수 있다.
\[ \Delta G_{\text{het}} = -V_S \Delta G_v + A_{SL} \gamma_{SL} + A_{SM} \gamma_{SM} - A_{SM} \gamma_{ML} \]
표면에너지항들이 왜 생겨났는지를 생각해보자. 각 표면이 발생함으로써 생긴 에너지 변화를 더하고 뺀 것이다.
기하적으로 Spherical cap에 관한 식을 다음과 같이 쓸 수 있다.
(이 역시 구에서 spherical cap에 관한 식을 유도해보자. 이건 쉽게 할 수 있다)
\[ V_S = \frac{4}{3} \pi r^3 \frac{(2 + \cos \theta)(1 - \cos \theta)^2}{4} \]
\[ A_{SL} = 2 \pi r^2 (1 - \cos \theta) \]
\[ A_{SM} = \pi r^2 \sin^2 \theta \]
이를 대입하면, 다음을 얻는다.
$$ \Delta G_{\text{het}} = \left\{ -\frac{4}{3} \pi r^3 \Delta G_v + 4 \pi r^2 \gamma_{SL} \right\} S(\theta) $$
$$ S(\theta) = \frac{(2 + \cos \theta)(1 - \cos \theta)^2}{4} = \frac{(2 - 3 \cos \theta + \cos^3 \theta)}{4} $$
저번 포스팅에서 다뤘던 Homogeneous Nucleation에서의 식을 떠올려보자.
$$ \Delta G_r = - \frac{4}{3} \pi r^3 \Delta G_V + 4 \pi r^2 \gamma_{SL} $$
Homogeneous 와 Heterogeneous Nucleation은 다음의 관계를 갖는다.
$$ \Delta G_{\text{het}} = S(\theta) \Delta G_{\text{hom}} $$
여기서 $ S(\theta) $ 식의 범위를 계산해보면, 다음과 같은 관계를 가지므로, (cos함수의 범위를 이용)
$$ 0 \leq S(\theta) \leq 1 $$
이 관계를 그래프로 그려보면 다음과 같다.
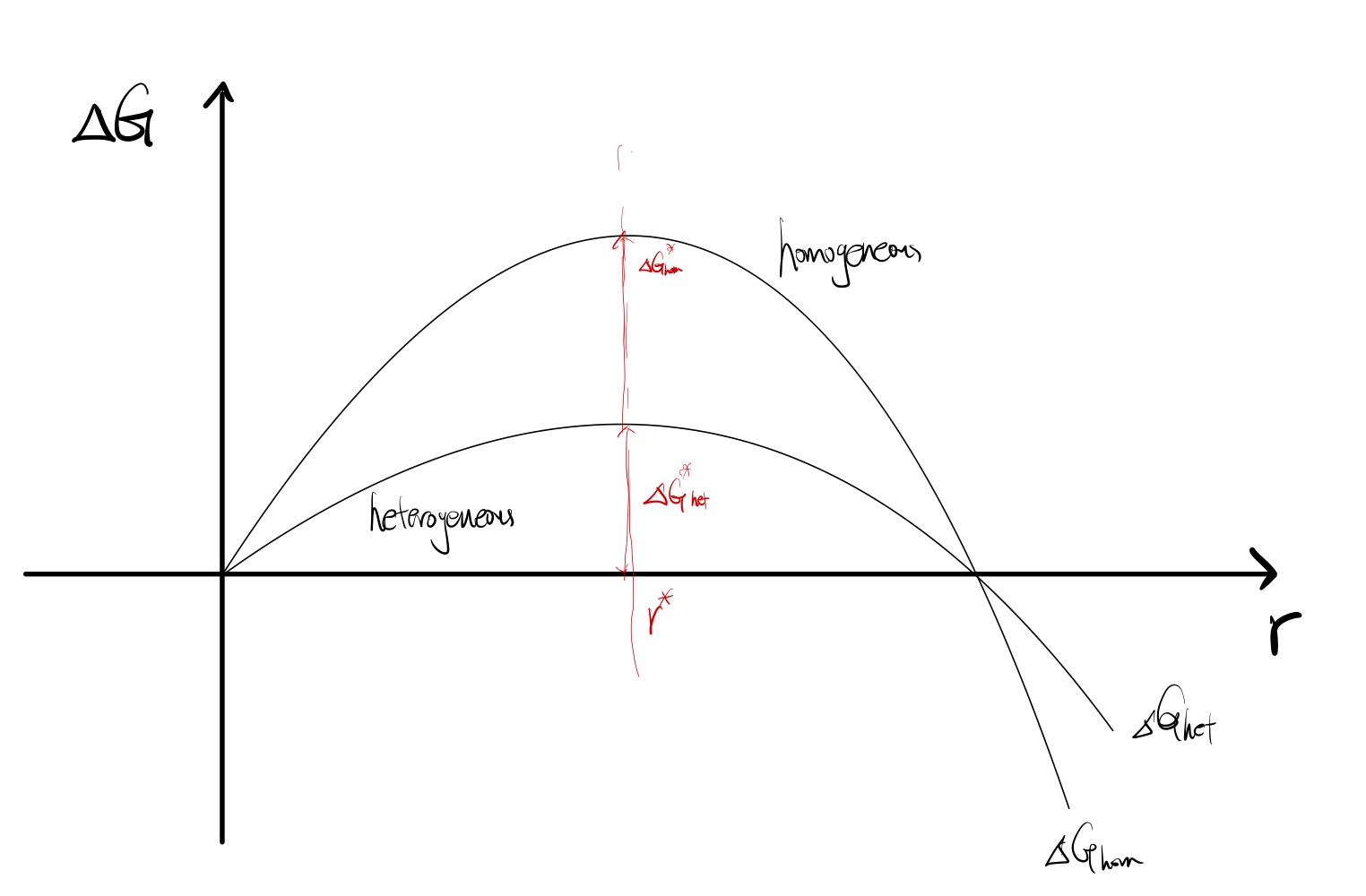
왼쪽 그래프는 $ \Delta G_{\text{het}} = S(\theta) \Delta G_{\text{hom}} $ 관계를 나타낸것이고,
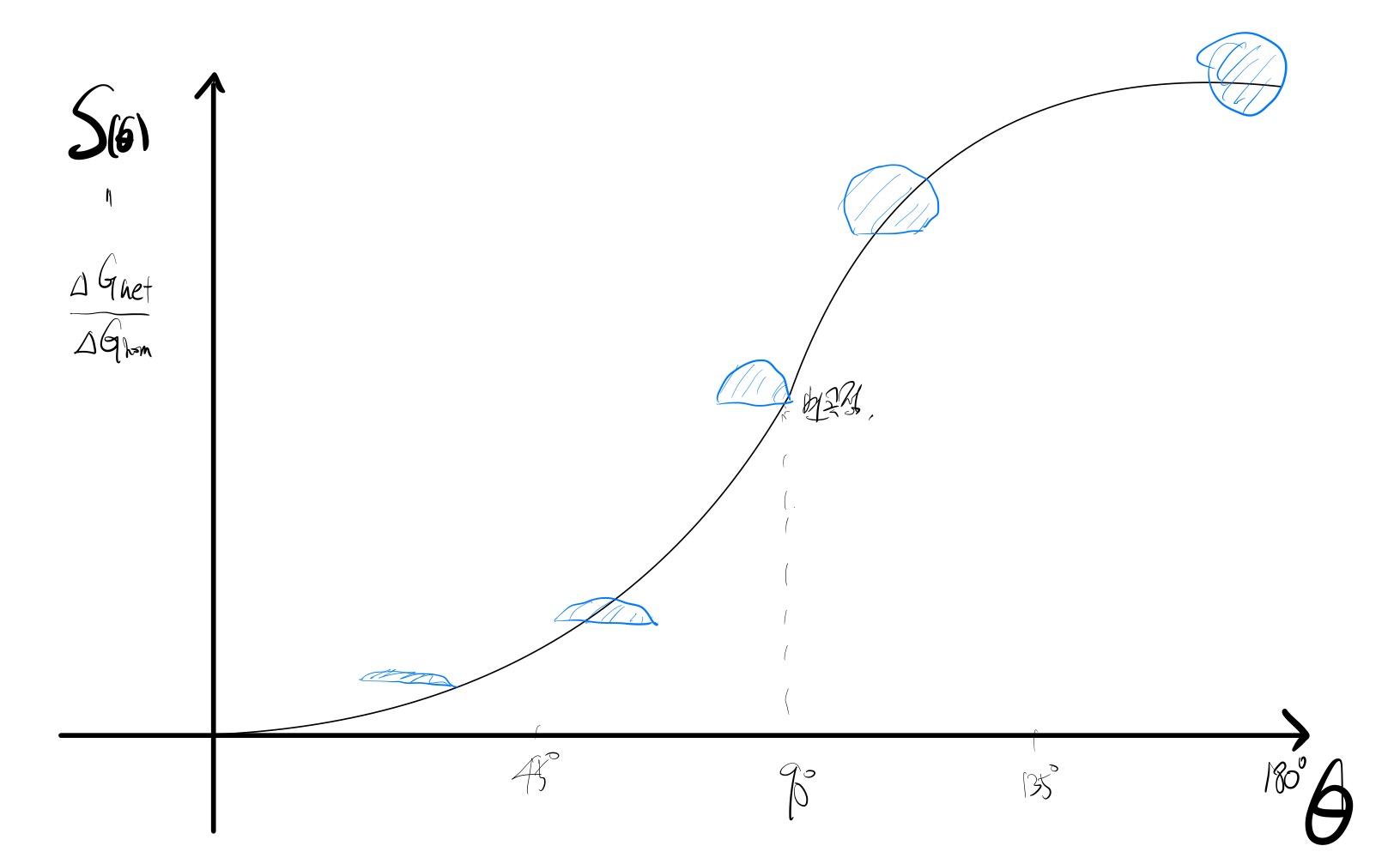
오른쪽 그래프는 $ S(\theta) $ 그래프를 그린 것이다.
$ S(\theta) $는 $ \theta $에만 종속적인 변수 이므로, $ \Delta G_{\text{het}} $와 $ \Delta G_{\text{hom}} $ 의 크기비율에만 관련있다.
즉, Heterogeneous Nucleation의 자유에너지 변화는 Homogeneous에 비해 작거나 같고,
r*의 위치나, x축 절편 등의 위치는 변화하지 않고, 두 그래프의 크기만 변화시킴을 알 수 있다.
뿐만 아니라, 접촉각 $ \theta $의 함수로 표현하면 (오른쪽), Solid의 모양을 파란색처럼 그릴 수 있다.
3. Heterogeneous Nucleation 장벽 $\Delta G^*_{\text{het}} $
우리는 지난 Homogeneous Nucleation 포스팅에서 보았듯,
Homogeneous Nucleation의 장벽(Barrier)는 다음의 관계를 가짐을 이미 알고 있다.
$$ \Delta G^*_{\text {hom}} = \frac{16 \pi \gamma_{SL}^3}{3 \Delta G_V^2} $$
그리고 지난 포스팅에서 Heterogeneous Nucleation의 자유에너지 변화를 이미 알고 있다.
이를 적용하면, Heterogeneous Nucleation에서의 장벽 $ \Delta G^*_{\text{het}} $을 계산할 수 있다.
\[ \begin{align} \Delta G^*_{\text{het}} &= S(\theta) \Delta G^*_{\text{hom}} \\ &= \frac{16 \pi \gamma_{SL}^3}{3 \Delta G_V^2} \cdot S(\theta) \\ &= \frac{16 \pi \gamma_{SL}^3}{3 \Delta G_V^2} \cdot \frac{(2 - 3 \cos \theta + \cos^3 \theta)}{4} \end{align} \]
4. 부피와 모양에 따른 $ \Delta G^*_{\text{het}} $
여기서 $ S(\theta) $ 의 기하학적 의미를 조금 더 생각해보자.
$ S(\theta) $는 구와 구 모자 (spherical cap) 사이의 부피관계와 같다.
수학적인 증명은 어렵지 않으니 생략하도록 하겠다. 직접 해보자.
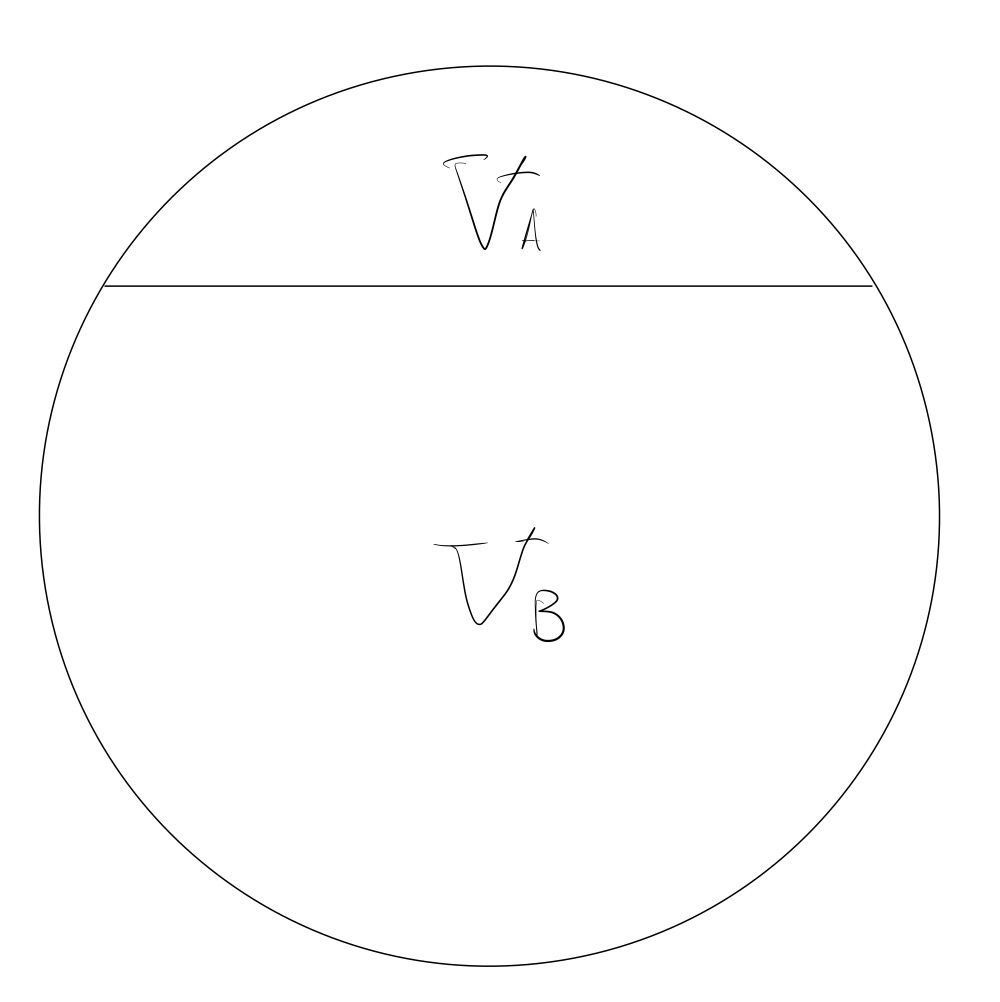
\[ \frac{V_A}{V_A + V_B} = \frac{2 - 3\cos \theta + \cos^3 \theta}{4} = S(\theta) \]
$ \Delta G^*_{\text{hom}} $는 mould 벽에 붙지 않은 완전한 구형일 때 계산한 결과이므로,
$ \Delta G^*_{\text{het}} $는 부피분율에 따라 계산되는 값임을 직관적으로도 이해할 수 있다.
$$ \Delta G^*_{\text{het}} = \frac{V_A}{V_A + V_B} \Delta G^*_{\text{hom}}$$
4.1 갈라진 틈 - Cresive 에서
이번에는 갈라진 틈(cresive) 사이에 solid가 형성되었다고 생각해보자.
cresive가 하나의 부채꼴모양이라고 한다면, 아래와 같은 그림을 그릴 수 있을 것이다.
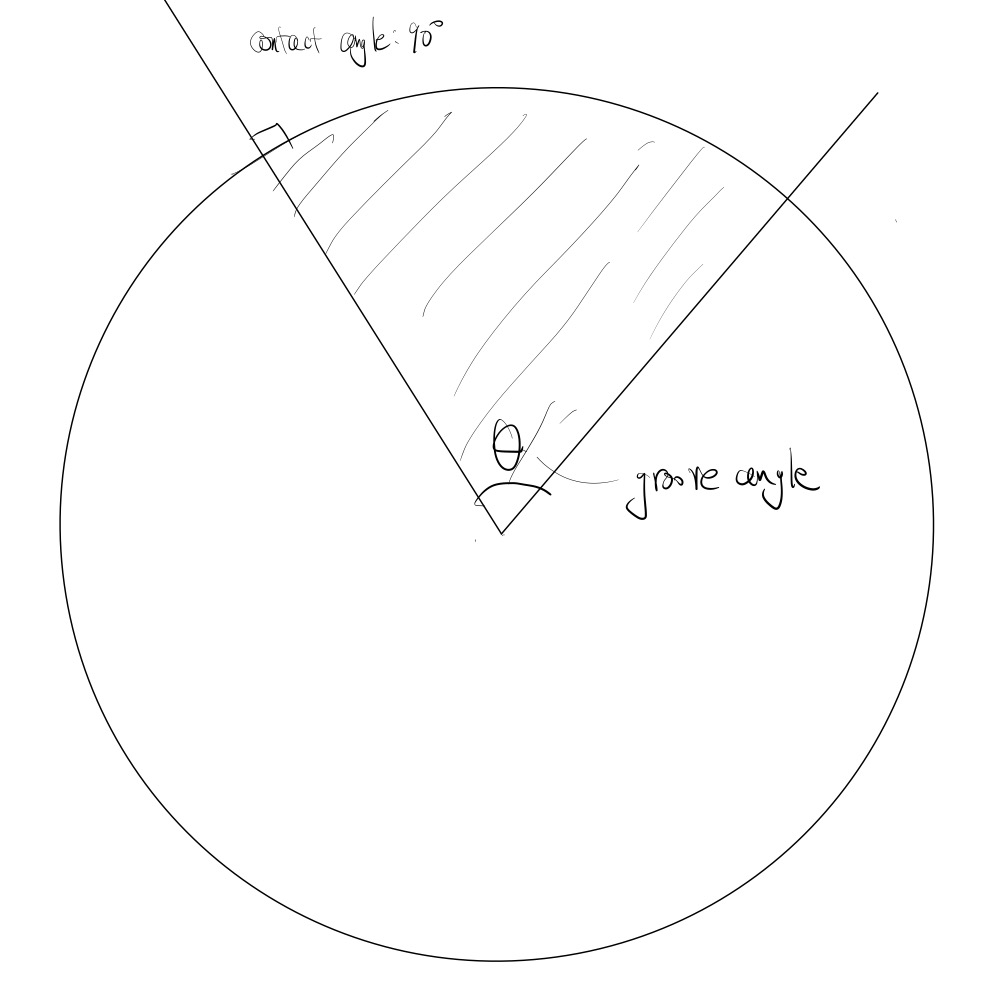
여기서 빗금친 부분이 Solid이다. 위의 식을 이용한다면, $ \Delta G^*_{\text{het}} $ 는 다음과 같이 쓸 수 있다.
$$ \Delta G^*_{\text{het}} = \frac{\theta}{360} \Delta G^*_{\text{hom}}$$
$ \theta $가 커질수록, $ \Delta G^*_{\text{het}} $가 커짐을 확인할 수 있는데,
이는 지난 포스팅에서 살펴보았던 관계( $ S(\theta) $ 와 $ \theta $ )와 일치한다.
4.2 일반적인 모양에서
일반적으로, 구형이 아닌 모양일 때, $ \Delta G_{\text{het}} $을 생각해보자.
기판 (Substrate - mould 표면이라 생각하면 되겠다) 위에 빗금친 영역만큼 Solid가 생성되었다.
이 때의 $ \Delta G^*_{\text{het}} $를 계산해보자. 아래와 같다.
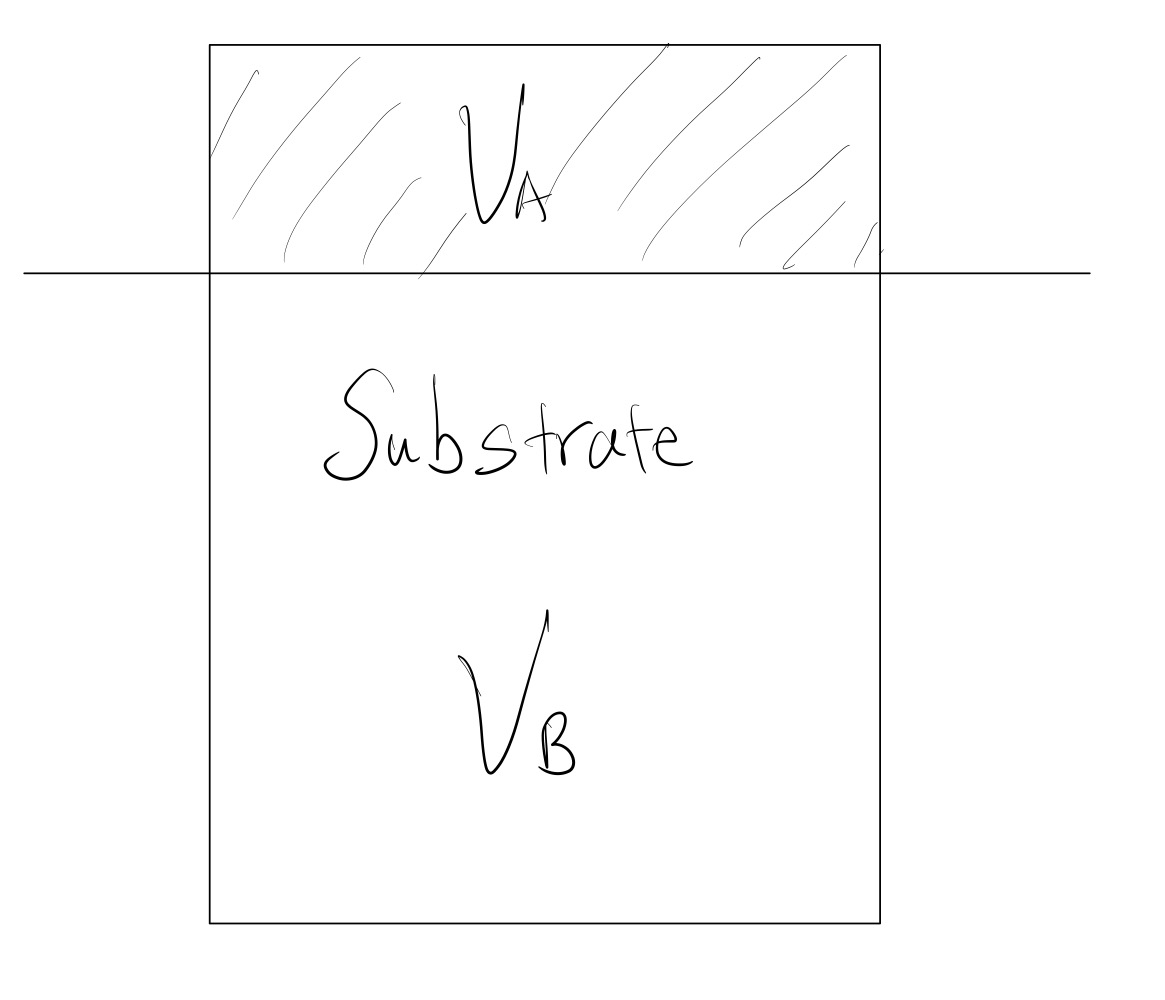
$$ \Delta G^*_{\text{het}} = \frac{V_A}{V_A + V_B} \Delta G^*_{\text{hom}}$$
즉, 부피가 커질수록 $ \Delta G^*_{\text{hom}} $에 가까워지는데,
이로부터 앞서 살펴보았던 경우와 모두 일맥상통하는 개념이라는 것을 알 수 있다.
참고로, 고체 위에 액체를 떨어뜨렸을 때 액체가 퍼지는 정도를 wetting이라 하는데,
부피가 작아질수록 good wetting이 된다는 것을 확인할 수 있다.
5. surface energy $ \gamma_{SM} $ 와 $ \Delta G^*_{\text{het}} $
위 1번에서 알아보았듯, 우리는 다음의 관계를 안다.
Heterogeneous와 Homogeneous Nucleation 은 같은 critical radius를 갖지만,
Heterogeneous Nucleation의 barrier가 더 낮다.
만약, Heterogeneous Nucleation에서 mould가 solid의 표면이 비슷하다면, 즉, $ \gamma_{SM} $이 낮다면,
\[ \gamma_{ML} = \gamma_{SL} \cos \theta + \gamma_{SM} \]
로부터, $ cos \theta $가 커지고, 이는 $ \theta $와 $ S(\theta) $ 가 더 작아진다는 의미이므로,
더 낮은 barrier를 갖게 될 것이다. 즉, $ \Delta G^*_{\text{het}} $가 낮아진다.
(이처럼, $ \theta $ 가 작아서, 표면에 잘 붙는 경우를 good wetting이라 한다.)
오늘 포스팅은 여기서 마친다.
다음포스팅에는 이어서, Heterogeneous Nucleation rate에 대해 다뤄보도록 하겠다.
궁금한 점이 있다면, 언제든 댓글로 질문을 달아주면 성실히 답변해보도록 하겠다.
그럼 안녕~!!

'전공 공부정리 > Phase Transformation (상변태)' 카테고리의 다른 글
| [PT] 2.2.2 Growth / Heat flow and Stability (Superheated & Supercooled) (1) | 2024.11.23 |
|---|---|
| [PT] 2.1.5 Heterogeneous Nucleation / rate (속도) (1) | 2024.11.23 |
| [PT] 2.1.3 Homogeneous Nucleation / rate (속도) (2) | 2024.11.23 |
| [PT] 2.1.2 Homogeneous nucleation - 2 (0) | 2024.11.23 |
| [PT] 2.1.1 Homogeneous Nucleation - 1 (0) | 2024.11.23 |



