상태 밀도 함수 (Density of State : DOS) in 1D, 2D, 3D 유도하기
오늘 포스팅에서는
상태 밀도 함수(DOS)를 유도하는 방법을 소개해보고자 한다.
상태 밀도 함수의 의미와 k-space에 대한 설명은 일단 생략하겠다.
(정말 죄송한 마음뿐이다. 시간이 허락하는 대로, 자세한 설명과 수식 타이핑을 할 수 있도록 하겠다.)
1D, 2D, 3D 각각의 DOS가 모두 다르니, 주의 깊게 봐주면 되겠다.
파일은 아래 다운받을 수 있도록 해두었다.
Free Electron의 Density of States (DOS) in 1D, 2D, 3D 유도하기
0. Free Electron의 파동함수가 갖는 Periodic Boundary Conditions
먼저, Free Electron의 파동함수를 간략하게 정리하고 넘어가자.
자세한 설명은 아래 포스팅에 디테일하게 정리해 두었으니,
이해가 어렵다면, 읽어보면 좋을 것 같다.
[고체물리] Free Electron의 슈뢰딩거 방정식 - 파동함수 & 분산관계 & k의 의미 (Periodic Boundary Conditions
Free Electron의 격자 내 슈뢰딩거 방정식 (Periodic Boundary Conditions) - 파동함수, 분산관계 (e-k relation), k의 의미까지 오늘 포스팅에서는 Nearly Free Electron Model을 설명함에 있어서, <..
gyuuuul.tistory.com
Periodic Boundary Conditions
결정은 주기적 성질을 가지므로, particle in a box 가 연속적으로, 반복적으로 존재한다.
따라서 슈뢰딩거 방정식과 boundary condition을 다음과 같이 세울 수 있다.
$ ( - \frac { \hbar ^ { 2 } } { 2 m } { \nabla ^ {2} } + U_{(r)})\; \psi _ { (r) } = E\; \psi_ (r) $, $ U_{(r)} = 0 $
- boundary condition
$$ \psi ( x , y , z ) = \psi ( x + L , y , z ) $$
$$ \psi ( x , y , z ) = \psi ( x , y + L , z ) $$
$$ \psi ( x , y , z ) = \psi ( x , y , z + L ) $$
이 해는 3차원 적으로 다음과 같이 주어진다.
$$ \psi _{k} ( r) = \frac{1}{\sqrt {V}} \; e^{i \; k \cdot r} $$
이 때, k는 벡터이고, 그 값 ($ k^{2}=k_{x}^{2} + k_{y}^{2} + k_{z}^{2} $) 은 아래와 같다.
$ k_{x} = \frac{2n_{x}\pi}{L_{x}} $
$ k_{y} = \frac{2n_{y}\pi}{L_{y}} $
$ k_{z} = \frac{2n_{z}\pi}{L_{z}} $
또한 eigenvalue를 풀었을 때 나오는, e-k relation(분산관계)는 아래와 같다.
$$ \epsilon _ { k } = \frac { \hbar ^ { 2 } k ^ { 2 } } { 2 m } $$
1. DOS in 3D
k - space를생각하자.

k-space Volume per k (k density)
$$ k-density = \frac {1}{\frac{2\pi}{L_{x}} \frac{2\pi}{L_{y}} \frac{2\pi}{L_{z}}} = \frac{V}{8 \pi^{3}} $$
$ g (k) d k $ 을 구하는 식을 세워보면,
구 껍질 속 number of state g(k) dk는 위 그림의 구 껍질 속에 있는 k의 개수의 두 배와 동일하므로,
1. k state에 up & down 스핀의 2개의 전자가 존재한다.
2. $ 4 \pi k ^ { 2 } d k $ 은 구 껍질 부피를 의미한다.
3. 위에서 구한 k density
위 셋을 곱하면 $ g (k) d k $ 을 구할 수 있다. 아래 식과 같다.
$$ g ( k ) d k = 2 \cdot \frac { V } { 8 \pi ^ { 3 } } \cdot 4 \pi k ^ { 2 } d k $$
k는의 에너지를 결정하는 값이므로 아래는 위 식과 다음과 같은 관계를 갖는다.
양변을 부피 V로 나눠주고(per Volume을 구하자) 적분해주면,
$$ \int g ( { \epsilon ) } d \epsilon = 2 \cdot \frac { 1 } { 8 \pi ^ { 3 } } \int 4 \pi k ^ { 2 } d k $$
$ \epsilon _ { k } = \frac { \hbar ^ { 2 } k ^ { 2 } } { 2 m } $ 에서,
$$ \frac { d \epsilon } { d k } = \frac { \hbar ^ { 2 } } { m } k $$
$$ d k = \frac { m } { k \hbar ^ { 2 } } d \epsilon $$
을 위 식에 대입해 주자. 그러면,
$$ \begin{align} \int g ( { \epsilon ) } d \epsilon & = \frac { 2 } { 8 \pi ^ { 3 } } \int 4 \pi \frac { m } { \hbar ^ { 2 } } \sqrt {\frac{2m \epsilon }{\hbar ^ { 2 } }} d \epsilon \\ & = \int \frac { m } { \pi ^ { 2 } \hbar ^ {2}} \sqrt {\frac{2m \epsilon }{\hbar ^ { 2 } }} d \epsilon \end{align} $$
$$ \therefore g ( { \epsilon ) } = \frac { m } { \pi ^ { 2 } \hbar ^ {2}} \sqrt {\frac{2m \epsilon }{\hbar ^ { 2 } }} $$
바로 이 $ g ( \epsilon ) $ 가 3D에서의 밀도함수 (Density of State)가 된다!!
(단, 초반에 Volume을 나눴던 것으로부터, 부피당 밀도함수라는 것을 유의하자)
2. DOS in 2D
아래 식을 유심히 살펴보자. 3D와마찬가지로 슈뢰딩거 방정식과 그 해는 차원이 하나 내려올 뿐 형태는 같다.
$$ (\frac { 1 } { \psi _ { x } } \frac { \partial ^ { 2 } \psi _ { x } } { \partial x ^ { 2 } } + k _ { x} ^ { 2 }) +(\frac { 1 } { \psi _ { y } } \frac { \partial ^ { 2 } \psi _ { y } } { \partial y ^ { 2 } } + k _ { y} ^ { 2 }) = 0 $$
여기서 각 괄호 안의 미분방정식이 0 이 되어야 하므로... 이를 풀어내게 되면,
$$ \psi _ { x } = \frac { 1 } { \sqrt { L_{x} } } e ^ { i k _ { x } \cdot x } \;\;\;\;\;\; k _{x}= \frac { 2 n_{x} \pi } { L_{ x} } $$
$$ \psi _ { y } = \frac { 1 } { \sqrt { L_{y} } } e ^ { i k _ { y } \cdot y } \;\;\;\;\;\; k _{y}= \frac { 2 n_{y} \pi } { L_{ y} } $$
$$ E_{n_{x} \cdot n_{y}} = \frac {\hbar ^ {2}} {2m} (k^{2}_{x}+k^{2}_{y}) $$
3D처럼 k-space를 생각하자. 당근, 이 경우엔 2D, 즉 좌표평면을 그려주면 된다.
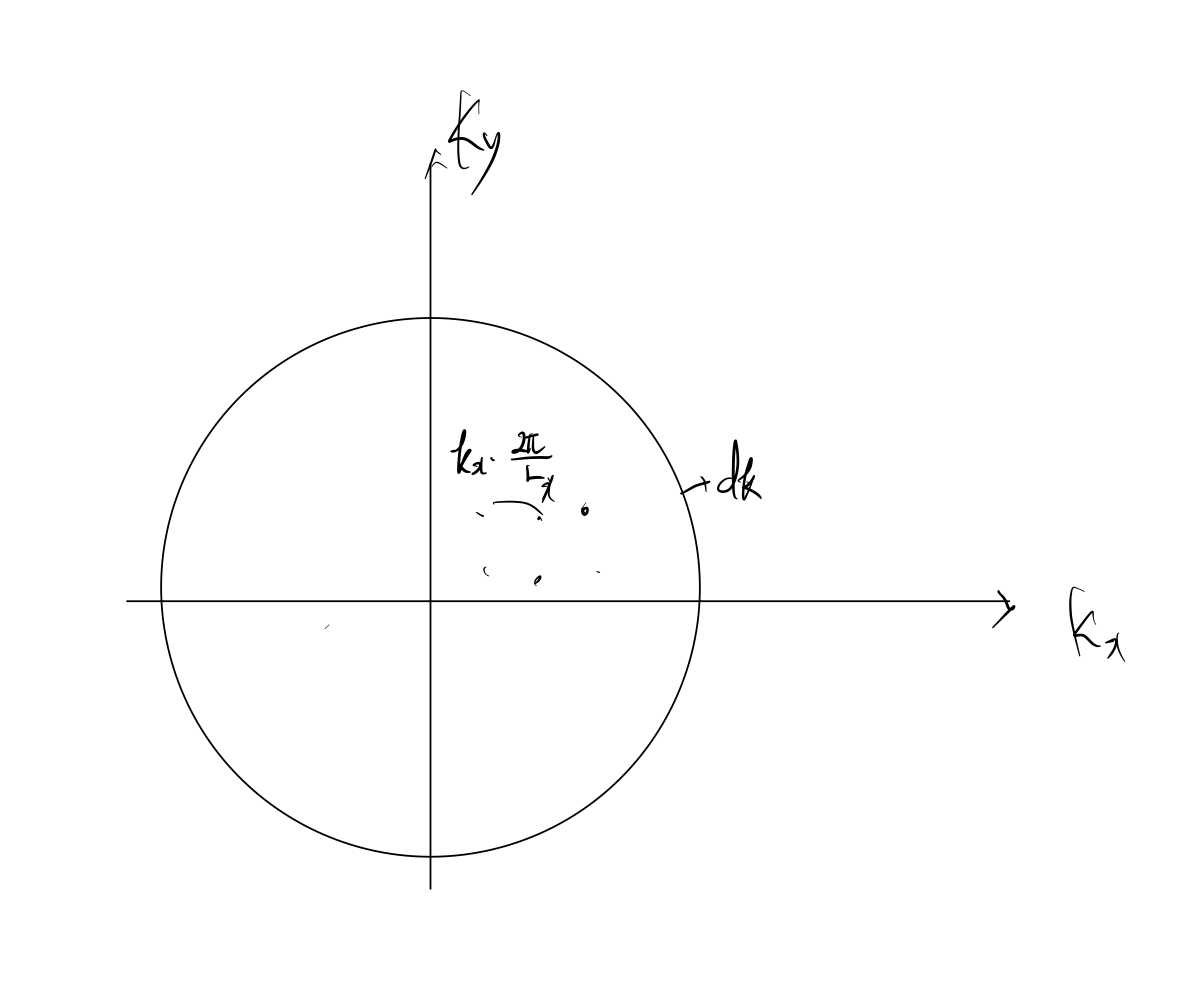
k space volume per k : k density는 아래와 같다.
$$ \frac {1}{V} = \frac { 1 } { \frac { 2\pi } {L_{x}} \frac { 2\pi } {L_{x}} } = \frac { V } { 4\pi^{2}} $$
이때, 원의 바깥쪽 number of state g(k) dk는위 그림의 원 바깥 쪽 속에 있는 k의 개수의 두 배와 동일하다. 앞선 식 (4)와 비슷하다.
$$ g ( k ) d k = 2 \cdot \frac { V } { 4 \pi ^ { 2 } } \cdot 2 \pi k d k $$
여기서 2는 1개의 state에 2개의 전자(up, down spin)가 존재한다는 것을 의미한다.
앞서 보았듯 k는 state의 에너지를 결정하는 값이었고, 이를 이용해 앞서 풀이와 비슷하게 다음을 얻는다.
$ \epsilon _ { k } = \frac { \hbar ^ { 2 } k ^ { 2 } } { 2 m } $ 에서, 다음을 대입하자.
$$ \frac { d \epsilon } { d k } = \frac { \hbar ^ { 2 } } { m } k $$
$$ d k = \frac { m } { k \hbar ^ { 2 } } d \epsilon $$
$$ \begin{align} \int g ( \epsilon ) d\epsilon &= 2 \cdot \frac { 1 } { 4 \pi ^ { 2 } } \cdot \int 2 \pi k d k \\ &= \int \frac {m}{\pi \hbar^{2}} d \epsilon \end{align} $$
$$ \therefore g ( \epsilon) = \frac {m} {\pi \hbar^{2}} $$
이 $ g ( \epsilon ) $ 가 2D에서의 밀도함수 (Density of State)가 된다!!
위의 3D에서의 밀도함수와 어떤 것이 다른지, 비교해 보자.
(이 경우 역시, Volume을 나눴던 것으로부터, 부피당 밀도함수라는 것을 유의하자)
3. DOS in 1D
앞선 식 (2)와 (3)을보자. 2D, 3D와마찬가지로 슈뢰딩거 방정식과 그 해는 차원이 하나 내려올 뿐 형태는 같다.
$$ \frac { 1 } { \psi _ { x } } \frac { \partial ^ { 2 } \psi _ { x } } { \partial x ^ { 2 } } + k _ { x} ^ { 2 } = 0 $$
$$ \psi _ { x } = \frac { 1 } { \sqrt { L_{x} } } e ^ { i k _ { x } \cdot x } \;\;\;\;\;\; k _{x}= \frac { 2 n_{x} \pi } { L_{ x} } $$
$$ E_{n_{x} } = \frac {\hbar ^ {2}} {2m} k^{2}_{x} $$
2D, 3D처럼 k space를생각하자. 이 경우엔 1D를 생각하면 되겠다.
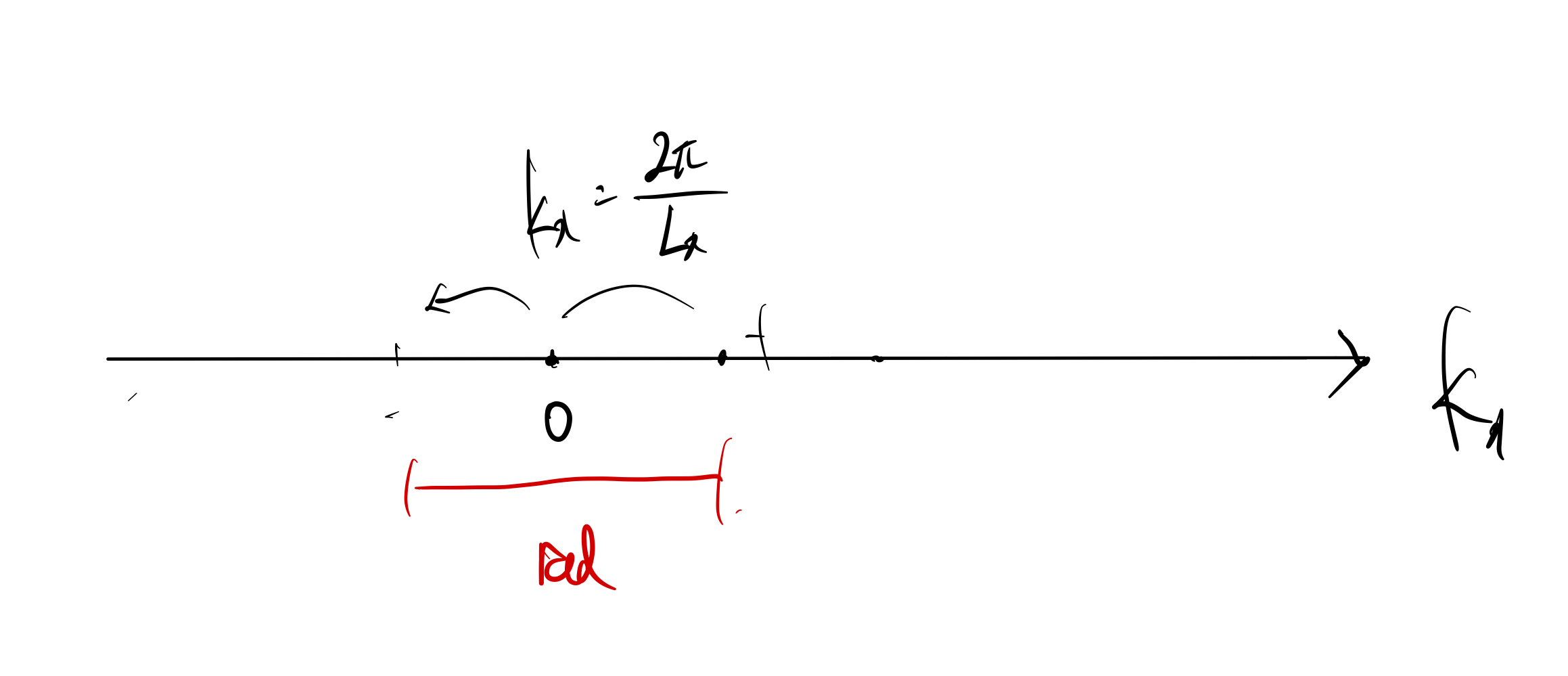
k space volume per k : k density는 아래와 같다.
$$ \frac { 1 } { V } = \frac { 1 } { \frac { 2 \pi } { L_{x} } } = \frac { V } { 2 \pi } $$
이때, 선의 number of state g(k) dk는위 그림의 선에 있는 k의 개수의 두 배와 동일하다. (3D, 2D와 마찬가지로)
$$ g ( k ) d k = 2 \cdot \frac { V } { 2 \pi } \cdot 2 d k $$
앞서 보았듯 k는 state의 에너지를 결정하는 값이었고, 이를 이용해 앞서 풀이와 비슷하게 다음을 얻는다.
$ \epsilon _ { k } = \frac { \hbar ^ { 2 } k ^ { 2 } } { 2 m } $ 에서, 다음을 대입하자.
$$ \frac { d \epsilon } { d k } = \frac { \hbar ^ { 2 } } { m } k $$
$$ d k = \frac { m } { k \hbar ^ { 2 } } d \epsilon $$
$$ \begin{align} \int g ( \epsilon ) d\epsilon &= 2 \cdot \frac { 1 } { 2 \pi } \cdot \int 2 d k \\ &= \int \frac {\sqrt{2}}{\pi \hbar} \sqrt{\frac{m}{\epsilon}} d \epsilon \end{align} $$
$$ \therefore g ( \epsilon) = \frac {\sqrt{2}}{\pi \hbar} \sqrt{\frac{m}{\epsilon}} $$
이 $ g ( \epsilon ) $ 가 1D에서의 밀도함수 (Density of State) 가 된다!!
위의 3D, 2D에서의 밀도함수와 어떤 것이 다른지, 비교해 보자.
(이 경우 역시, Volume을 나눴던 것으로부터, 부피당 밀도함수라는 것을 유의하자)
이렇게 오늘 포스팅에서는 상태밀도함수 (Density of State)에 대해 알아보았다.
고체물리에서 정말정말 중요한 내용인 만큼, 꼭 기억해두었으면 하는 내용이라,
열심히 포스팅해 보았다.
내용 중 질문 사항이 있다면,
언제든지 댓글로 달아주면 친절히 답변할 수 있도록 하겠다.
그럼 다음 포스팅에서 만나는걸루 하고
모두 안녕~~!!

'전공 공부정리' 카테고리의 다른 글
| [양자역학 기초지식] 에르미트 행렬과 브라-켓(bra-ket)표기법 & 해밀토니안의 행렬 표현 (0) | 2024.04.25 |
|---|---|
| [고체물리] 유효 질량 (effective mass) 구하기, 물리적 의미 & 유도하는 법 알아보기 (0) | 2024.04.13 |
| [고체물리] 블로흐 정리 (Bloch Theorem) 유도하기 (2) | 2024.03.29 |
| [통계역학] Bose-Einstein 분포 함수 유도 (0) | 2024.03.20 |
| [통계역학] Fermi-Dirac 분포 함수 유도하기 (0) | 2024.03.06 |



